二相混合式步进电机控制方式的研究现状
电机的数学模型是控制算法的基础,步进电机的数学模型也是因为数学理论的成熟逐渐发展起来,其中Singh-Kuo模型是有代表性的模型,这个模型忽略了磁滞和涡流损耗,假设相绕组中产生的磁链随转子位置角按正弦规律变化,绕组电感与转子位置无关等;之后出现了较S ingh-Ku。的改进型的Pickup-Russell模型,该模型认为绕组磁链是绕组电流和转子位置的函数[0l; A.C.Leenhouts等人借鉴Pickup-Russell模型将绕组磁链随电流变化关系用电感系数来表示,提出Leenhouts模型 。
混合式步进电机系统的性能很大程度取决于控制器的优劣,从前述可以看到步进电机主要有开环、闭环、矢量和智能控制等控制方式。开环控制使用方便,系统构成简单且成本低,在精度要求不太高的场合有着广泛的应用,至今也没有合适的替代产品。但如前所说,这种方式存在一个振荡的区域,尤其是低速运行时接近电机的共振区,此时振动和噪声都比较大。但是对开环控制的改进也是不断地在进行中,自1975年美国学者T. R. Frederickson首次在美国增量运动控制系统及器件年会上提出了步进电机步距角细分的控制方法后[ysl,随着微电子和电力电子技术的发展,当前世界上混合式步进电机新技术正处在高速的发展之中,智能控制的V}想进入了步进电机的驱动控制领域,还出现了具有实时可变的细分一功能驱动控制电路。通过这些年的发展,步进电机控制方式逐渐形成了升频升压控制,恒流斩波控制,细分控制,矢量控制,位置、速度反馈控制等控制方式,但是新型控制方式的运用还不成熟,也没有出现相关产品,而国内虽然研究上取得很大进步但不管是控制器还是控制软件上看,和国外还有一定的差距。目前国内外混合式步进电机控制系统在实际中主要有:基于微控制器设计的专用集成芯片,基于单片机微处理器等,基于CPLD和PFGA和基于 DSP实现的控制系统,随着各个新型控制方式的出现,将高运算速度、功能强大的DSP应用到控制器当中,也是目前研究的热点方向
而随着神经网络技术的发展,对于混合式步进电机这种数学模型难以得到的电机来说,神经网络却提供了良好的控制工具。神经网络是一种能自学习及自适应不确定系统的智能控制方法,它对很复杂的非线性系统都可以在很大程度上逼近模拟,并具有极好的容错性和鲁棒性,所以随着神经网络技术的不断发展,各项研究也开始越来越多地关注其在步进电机系统中的应用。有研究将神经网络用于实现步进电机最佳细分电流,在学习中使用Bayes正则化算法,使用权值调整技术避免多层前向神经网络陷入局部极小点,有效解决了等步距角细分问题。2100433B
二相混合式步进电机造价信息
因为在实际的应用当中,步进电机为伺服系统的执行元件,所以设计中比较注重位置定位精确和产生较大转矩等方面,从而在定转子的设计中均为凸极结构并会在极上开有小齿,造成了气隙磁场存在着较大的空间谐波,从而导致电机的转矩脉动和转速波动也会比较大,容易产生噪声以至于振荡。由于混合式步进电机的气隙磁场分别是由转子永磁体和定子励磁绕组产生的,所以受磁路饱和的影响,当二者相互加强的时候,合成的磁通通常是小于两者的线性叠加,这时电机的磁场处于过饱和状态,运行效率比较低。另外从混合式步进电机的矩频特性可以看出,在转速达到一定数值后,输出转矩会很明显的下降,容易失步,有关学者曾就此做了研究提出了降低电流参考值的处理方法,但是也只有一定效果,进一步还提出了减少匝数、增大电流的解决方案,还有人为了增大步进电机高频时的输出转矩提出了减小电机绕组的L/R时间常数的方法 。
这些问题也归结为一个振荡和失步的问题。振荡的根本原因是转子到达平衡位置是还有多余的动能,对于此问题,一般采用阻尼和细分控制技术就可以达到较好的输出效果,有些国外的学者通过建立共振检测模型,调节励磁绕组电流的方、法来改善步进电机的这个问题,还有在对步进电机绕组电流中的谐波分量进行分析过后,通过建立共振阀值模型来对绕组电压进行补偿的办法。而失步的问题有研究显示,转子速度慢于步进电机旋转磁场速度、步进电机及所带负载存在的惯性、步进电机产生的共振等这些现象是严生失步的原因,可以通过优化步进电机的加减速曲线,有效的应对惯性转矩对失步产生的影响,还有采用细分控制技术解决这类问题。
从上述问题可以看出,混合式步进电机因其控制方面的要求,在设计电机本体的时候就对于电机的谐波控制、运行时的稳定性能方面考虑较少,所以在高速运行时转矩的下降会很快,同时工作时的运行效率变低,转矩脉动比较明显,造成较大的电机转速波动和振动噪声。但是上述问题提到的一些解决方法都是属于步进电机开环控制方式下的优化措施,这样的条件下忽略了转子永磁体产生的磁场对合成磁场发挥的作用,控制的效果并不是很好,所以在这种情况下采用其他控制方式则是另一个比较好的手段。
当两相控制绕组按AA BB或BB AA的次序轮流通电,侮拍只有一相绕组通电,四拍构成一个循环。当控制绕组有电流通过时,便产生磁动势,它与永久磁钢产生的磁动势相互作用,产生电磁转知,使转子产生步进运动。
当A相绕组通电时,在转子N极端磁极1上的绕组产生的S磁极吸引转子N极,使得磁极1下是齿对齿,磁力线由转子N极指向磁极1的齿面,磁极5下也是齿对齿,磁极3和7是齿对槽。由于两段转子铁芯上的小齿相互错开半个齿距,在转子S极端,磁极1'和5’产生的S极磁场,排斥转子S极,与转子正好是齿对槽,磁极3’和7’齿面产生N极磁场,吸引转子S极,使得齿对齿。
因转子上共有50个齿,其齿距角为3600 /50=720_宁子仇个极即所占的街数为不是整数,因此当定子的A相通电,在转子N极,磁极1的5个齿与转子齿对齿,旁边的B相绕组的磁极2的5个齿和转子齿有1/4齿距的错位,即1.80,A相磁极3的齿和转子就会错位3.6 0,实现齿对槽了。磁力线是沿转子N端~A(1)S磁极~导磁环~A(3' )N磁极~转子S端~转子N端,成一闭合曲线。当A相断电B相通电时,磁极2产生N极性,吸合离它最近的S极转子7齿,使得转子沿顺时针方向转过1.80,实现磁极2和转子齿对齿,此时磁极3和转子齿有1/4齿距的错位。依次类推若继续按四拍的顺序通电,转子就按顺时针方向一步一步地转动,侮通电一次即侮来一个脉冲转子转过1.80,即称步距角为1.80,转子转过一圈需要3600 /1.80 =200个脉冲 。
在转子S极端也是同样道理,当绕组齿对齿时,其旁边一相磁极错位1.803步进电机驱动器步进电机必须有驱动器和控制器才能正常工作。驱动器的作用是对控制脉冲进行环形分配、功率放大,使步进电机绕组按一定顺序通电,控制电机转动。
步进电机42BYG250C的驱动器为SH20403。为lOV} 40V直流供电,A , A-,B , B-端子要连接步进电机的四条引线,DC , DC-端子接驱动器工作直流电源,输入接口电路包括公共端(接输入端子电源正极)、脉冲信号输入端(输入一系列脉冲,内部分配以驱动步进电机A,B相)、方向信号输入端(可实现步进电机的正、反转)、脱机信号输入端 。
步进电机驱动器输入端子功能:
公共端:将输入信号的电源正极连接到该端子上,为CP,DIR, FREE端子提供,此时对应的内部光祸导通,控制信号输入驱动器中。
脉冲信号输入CP:此端子和57-200的高速脉冲输出端(Q0.0或Q0.1)相连,以发出连线高速脉冲驱动步进电机。
方向信号输入DIR:此端子和57-200的输出端Q0.2相连,其高电平和低电平控制电机的两个转向。
脱机信号FREE:此端为低电平有效,这时电机处于无力知状态
二相混合式步进电机控制方式的研究现状常见问题
-
反应式步进电机:一般为三相,可实现大转矩输出; 混合式步进电机:是指混合了永磁式和反应式的优点的电机,它又分为两相和五相。这是目前应用最广泛的一种步进电机。
-
步进电机分三种:永磁式(PM) ,反应式(VR)和混合式(HB)。 反应式步进一般为两相,转矩和体积较小,步进角一般为7.5度 或1.5度;永磁式步进一般为三相,可实现大转矩输出,步进角一般为1.5度...
-
步进电机分三种:永磁式(PM) ,反应式(VR)和混合式(HB)。反应式步进一般为两相,转矩和体积较小,步进角一般为7.5度 或1.5度;永磁式步进一般为三相,可实现大转矩输出,步进角一般为1.5度,...
工业控制中采用的定子磁极上带有小齿,转子齿数很多的结构,其步距角可以做得很小。图2混合式步进电机绕组接线图中A,B两相绕组沿径向分相,沿着定子圆周有8个凸出的磁极,1,3,5,7磁极属于A相绕组,2, 4, 6, 8磁极属于B相绕组,定子侮个极面上有5个齿,极身上有控制绕组。转子由环形磁钢和两段铁芯组成,环形磁钢在转子中部,轴向充磁,两段铁芯分别装在磁钢的两端,使得转子轴向分为两个磁极。转子铁芯上均匀分布50个齿,两段铁芯上的小齿相互错开半个齿距,定转子的齿距和齿宽相同 。
混合式步进电动机内部结构特殊,是一类高度非线性的机电装置。 1986年Hanselman采用磁场的“磁网络单元法”来计算反应式步进电机的磁场。1988年,G Heine提出了精确的混合式步进电机的等值磁网络模型,首次在模型中考虑了定子极间漏磁通,每极边缘转矩对电机矩角特性及步距误差的影响,分析了四相混合式步进电机谐波转矩对电机矩角特性及步距误差的影响,但是这种模型耗费的机时量仍然很大 。
为简化数学分析, 沿用G.Heine提出的混合式步进电机等值磁网络模型,以典型的二相八极混合式步进电动机,忽略铁心饱和和高次谐波对电机磁系统的影响 (铁心饱和和高次谐波往往是步进电机极限运行时的状况,正常运行时,不会对定性分析的结论有原则性的影响),建立了分析细分驱动的简化基本数学模型。混合式步进电动机绕组电感参数的特点与普通电机有区别,具有轴向和径向混合的磁系统,定转子双凸结构。在二相混合式步进电机磁网络模型简化磁路图中,定子八个极中在直径上相对的两个极的电磁状态完全相同,可以合并。这样电机的每一端只有4条支路。
步进电机作为执行元件,是机电一体化的关键产品之一,广泛应用在各种自戴化设备中。
步进电机是将电脉冲信号转变为角位移或线位移的开环控制元件。当步进驱私器接收到一个脉冲信号,它就驱动步进申机按设定的方向转动一个固定的角度(即步进角)。可以通过控制脉冲个数来控制角位移量,从而达到准确定位的目的。
混合式步进电机由定子和转子两部分组成。常见的定子有8个极或4个极,极面上均匀分布一定数量的小齿;极上线圈能以两个方向通电,形成A相和万相,B相和B相。它的转子也由圆周上均布一定数量小齿的两块齿片等组成。这两块齿片相互错开半个齿距。两块齿片中间夹有一只轴向充磁的环形永久磁钢。显然,同一段转子片上的所有齿都具有相同极性,而两块不同段的转子片的极性相反。混合式步进电机的结构图如图3-1.图3-2是四相混合式步进电机以圆周展开的剖面模型。图3-2上图是转子S极所出的剖面图,图3-2下图是N极剖面图。图3-2中,定子齿距和转子齿距相同。先考虑磁极I和磁极IB下面的磁场。定子线圈通电后,磁极I产生N极,磁极m产生S极 。
因为N极这段的转子齿和S极转子齿相互错开半个齿距,所以,仅靠定子电流磁场并不能向磁阻式电机那样产生有意义的转矩。但是,把永久磁钢产生的磁场叠加上去,情况就不一样了。因为磁极I下面的两冷磁场相互增强,因此产生向左的驱动力;而磁极m下面的两个分量相互抵消,向右的力大大削弱。再看图3-2下图,磁极m下面的定子磁场和转子磁场方向相同,磁极I下面的磁场方向相反,最终得到向左的合力。转子在驱动力的作用下将转过工齿距,驱动力降为零,达到平衡位置。
如果切断磁极I、III的激磁,同时向磁极II , IV上的线圈通入电流,分别产生S极和N极。转子将向左再走一步。按照特定的时序激磁,如A-B -A -B-A-"',电机就能沿逆时针方向连续旋转。改变激磁时序,以A-B-A-B-A-…激磁,电机将沿顺时针方向连续旋转。
二相混合式步进电机控制方式的研究现状文献

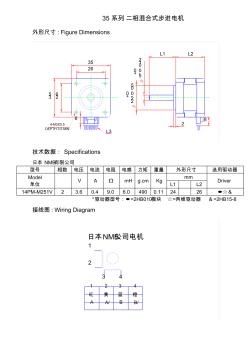 35系列二相混合式步进电机
35系列二相混合式步进电机
35系列二相混合式步进电机 外形尺寸 : Figure Dimensions 35 26 35 26 4-M3X0.5 DEPTH 3.5 MIN 6 5+ 0 -0 .0 12 22 +0 -0 .0 5 2 8 L1 L2 L3 技术数据: Specifications 日本 NMB有限公司 型号 相数 电压 电流 电阻 电感 力矩 重量 外形尺寸 选用驱动器 Model 单位 V A Ω mH g.cm Kg mm Driver L1 L2 14PM-M251V 2 3.6 0.4 9.0 6.0 490 0.11 24 26 ●☆& *驱动器型号:●=2HB010模块 ☆=两维驱动器 &=2HB15-8 接线图 : Wiring Diagram 1 2 3 4 1 2 43 橙蓝黄红 A A/ B B/ 日本NMB公司电机 39系列二相混合式步进电机 外形尺寸 : Fi

 35系列二相混合式步进电机(20201019152927)
35系列二相混合式步进电机(20201019152927)
35 系列二相混合式步进电机 外形尺寸 :Figure Dimensions 35 26 35 26 4-M3X0.5 DEPTH 3.5 MIN 6 5+ 0 -0 .0 12 22 +0 -0 .0 5 2 8 L1 L2 L3 技术数据: Specifications 日本 NMB 有限公司 型号 相数 电压 电流 电阻 电感 力矩 重量 外形尺寸 选用驱动器 Model 单位 V A Ω mH g.c m Kg mm Driver L1 L2 14PM-M251V 2 3.6 0.4 9.0 6.0 490 0.11 24 26 ●☆& *驱动器型号:●=2HB010 模块 ☆=两维驱动器 & =2HB15-8 接线图 :Wiring Diagram 1 2 3 4 1 2 43 橙蓝黄红 A A/ B B/ 日本NMB公司电机 39 系列 二相混合式步进电机 外形
二相混合式步进电机
DV245是基于DSP控制的二相混合式步进电机驱动器,是新一代数字式步进电机驱动器。驱动电运行平稳,震动和噪音极小。定位精度最高可达40000步/转。该产品广泛应用于雕刻机、中型数控机床、电脑绣花机、包装机械等分辨率较高的小、中型数控设备上。
步进电机PID 控制
PID 控制作为一种简单而实用的控制方法 , 在步进电机驱动中获得了广泛的应用。它根据给定值 r( t) 与实际输出值 c(t) 构成控制偏差 e( t) , 将偏差的比例 、积分和微分通过线性组合构成控制量 ,对被控对象进行控制 。文献将集成位置传感器用于二相混合式步进电机中 ,以位置检测器和矢量控制为基础 ,设计出了一个可自动调节的 PI 速度控制器 ,此控制器在变工况的条件下能提供令人满意的瞬态特性 。文献根据步进电机的数学模型 ,设计了步进电机的 PID 控制系统 ,采用 PID 控制算法得到控制量 ,从而控制电机向指定位置运动 。最后 ,通过仿真验证了该控制具有较好的动态响应特性 。采用 PID 控制器具有结构简单 、鲁棒性强 、可靠性高等优点 ,但是它无法有效应对系统中的不确定信息 。
目前 , PID 控制更多的是与其他控制策略相结合 , 形成带有智能的新型复合控制 。这种智能复合型控制具有自学习 、自适应 、自组织的能力 ,能够自动辨识被控过程参数 , 自动整定控制参数 , 适应被控过程参数的变化 ,同时又具有常规 PID 控制器的特点。
步进电机自适应控制
自适应控制是在 20 世纪 50 年代发展起来的自动控制领域的一个分支 。它是随着控制对象的复杂化 ,当动态特性不可知或发生不可预测的变化时 ,为得到高性能的控制器而产生的 。其主要优点是容易实现和自适应速度快 ,能有效地克服电机模型参数的缓慢变化所引起的影响 ,是输出信号跟踪参考信号 。文献研究者根据步进电机的线性或近似线性模型推导出了全局稳定的自适应控制算法 , 这些控制算法都严重依赖于电机模型参数 。文献将闭环反馈控制与自适应控制结合来检测转子的位置和速度 , 通过反馈和自适应处理 ,按照优化的升降运行曲线 , 自动地发出驱动的脉冲串 ,提高了电机的拖动力矩特性 ,同时使电机获得更精确的位置控制和较高较平稳的转速 。
目前 ,很多学者将自适应控制与其他控制方法相结合 ,以解决单纯自适应控制的不足。文献设计的鲁棒自适应低速伺服控制器 ,确保了转动脉矩的最大化补偿及伺服系统低速高精度的跟踪控制性能 。文献实现的自适应模糊 PID 控制器可以根据输入误差和误差变化率的变化 ,通过模糊推理在线调整 PID参数 ,实现对步进电机的自适应控制 ,,从而有效地提高系统的响应时间 、计算精度和抗干扰性 。
步进电机矢量控制
矢量控制是现代电机高性能控制的理论基础 ,可以改善电机的转矩控制性能 。它通过磁场定向将定子电流分为励磁分量和转矩分量分别加以控制 ,从而获得良好的解耦特性 ,因此 ,矢量控制既需要控制定子电流的幅值 ,又需要控制电流的相位 。由于步进电机不仅存在主电磁转矩 ,还有由于双凸结构产生的磁阻转矩 ,且内部磁场结构复杂 , 非线性较一般电机严重得多 , 所以它的矢量控制也较为复杂 。推导出了二相混合式步进电机 d-q 轴数学模型 ,以转子永磁磁链为定向坐标系 ,令直轴电流 id =0 ,电动机电磁转矩与 iq 成正比 , 用PC 机实现了矢量控制系统 。系统中使用传感器检测电机的绕组电流和转自位置 ,用 PWM 方式控制电机绕组电流 。文推导出基于磁网络的二相混合式步进电机模型 , 给出了其矢量控制位置伺服系统的结构 ,采用神经网络模型参考自适应控制策略对系统中的不确定因素进行实时补偿 ,通过最大转矩/电流矢量控制实现电机的高效控制 。
步进电机智能控制的应用
智能控制不依赖或不完全依赖控制对象的数学模型 ,只按实际效果进行控制 ,在控制中有能力考虑系统的不确定性和精确性 , 突破了传统控制必须基于数学模型的框架 。目前 , 智能控制在步进电机系统中应用较为成熟的是模糊逻辑控制 、神经网络和智能控制的集成 。
模糊控制
模糊控制就是在被控制对象的模糊模型的基础上 ,运用模糊控制器的近似推理等手段 ,实现系统控制的方法 。作为一种直接模拟人类思维结果的控制方式 ,模糊控制已广泛应用于工业控制领域 。与常规控制相比 ,模糊控制无须精确的数学模型 , 具有较强的鲁棒性 、自适应性 , 因此适用于非线性 、时变 、时滞系统的控制 。给出了模糊控制在二相混合式步进电机速度控制中应用实例 。系统为超前角控制 ,设计无需数学模型 ,速度响应时间短 。
神经网络控制
神经网络是利用大量的神经元按一定的拓扑结构和学习调整的方法 。它可以充分逼近任意复杂的非线性系统,能够学习和自适应未知或不确定的系统 ,具有很强的鲁棒性和容错性,因而在步进电机系统中得到了广泛的应用 。将神经网络用于实现步进电机最佳细分电流 ,在学习中使用 Bayes 正则化算法 ,使用权值调整技术避免多层前向神经网络陷入局部极小点 ,有效解决了等步距角细分问题 。
- 相关百科
- 相关知识
- 相关专栏
- 二箱式冷热冲击试验机
- 二级国家注册建造师
- 二级安全评价师考试易考宝典软件
- 二级建筑工程管理与实务过关必做习题集
- 二级建筑师考试
- 二级建筑师
- 二级建筑
- 二级建设工程施工管理过关必做1000题
- 二级建设工程法规及相关知识过关必做1000题
- 二级建造师 2019建设工程施工管理真题汇编及解析
- 二级建造师 2019建设工程施工管理考前冲刺试卷
- 二级建造师《建设工程施工管理》过关必做1000题
- 二级建造师助手
- 二级建造师历年考试真题
- 二级建造师建设工程法规及相关知识题库
- 二级建造师执业资格考试大纲(矿业工程专业2007年版2G300000)
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 可替代现有隔热保温材料的新型材料
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 中国工程造价咨询业的发展趋势
- 支持并行工程和智能CAPP的制造资源建模技术
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 在“建筑节能与居住舒适”专题技术交流会议上的讲话
- 以MSP430FW427为核心的远程数字水表设计