电路理论:时域与频域分析内容简介
《电路理论:时域与频域分析》立论严谨、概念清晰、要点突出、叙述流畅、例题丰富、便于自学。可作为高等院校电类有关专业的教材或教学参考书,也可供有关技术人员参考。
电路理论:时域与频域分析造价信息
第1章 动态元件和动态电路
1-1 单位阶跃函数与单位冲激函数
1-2 电容元件
“电容元件”是“电路分析”学科中电路模型中除了电阻元件R,电感元件L以外的一个电路基本元件。在线性电路中,电容元件以电容量C表示。元件的“伏安关系”是线性电路分析中除了基尔霍夫定律以外的必要的约束条件。电容元件的伏安关系是 i=C(dv/dt),也就是说,电容元件中的电流,除了电容量C以外,与电阻元件R不同,它不是取决于电压v本身,而是取决于电压对时间的变化率(dv/dt).电压变化愈快,电容中的电流愈大,反之则愈小。据此,在“稳态”情况下,当电压为直流时,电容中电流为零;当电压为正弦波时,电容中电流也是正弦波,但在相位上要超前电压(π/2);当电压为周期性等腰三角形波时,电流为矩形波,如此等等。总的来说,电容中的电流波形比电压变化得更快,含有更多的高频成分。
1-3 电感元件
电感元件是一种储能元件,电感元件的原始模型为导线绕成圆柱线圈。当线圈中通以电流i,在线圈中就会产生磁通量Φ,并储存能量。表征电感元件(简称电感)产生磁通,存储磁场的能力的参数,也叫电感,用L表示,它在数值上等于单位电流产生的磁链。电感元件是指电感器(电感线圈)和各种变压器。
1-4 动态电路
1、动态电路是指含有储能元件L、C的电路。
2、动态电路是指含有储能元件的电路。
3、 当动态电路状态发生改变时需要经历一个变化过程才能达到新的稳定状态。这个变化过程成为电路的过渡过程;
4、描述动态电路的电路方程为微分方程;
5、动态电路方程的阶数通常等于电路中动态元件的个数。
本章小结
习题一
第2章 一阶电路与二阶电路
2-1 一阶电路的两种基本类型
2-2 一阶电路的零输入响应
2-3 一阶电路的零状态响应
2-4 全响应
换路后,电路中即存在激励电源,储能元件又有初始储能,他们共同维持的响应。
全响应(complete response)是零输入响应和零状态响应叠加的结果,也体现了线性电路的叠加性.
2-5 求解一阶电路的三要素法
2-6 单位冲激响应
2-7 任意波形激励下的零状态响应
2-8 二阶电路
含有两个独立的动态元件的线性电路,要用线性,常系数二阶微分方程来描述,故称为二阶电路。
系统的响应除了激励所引起外,系统内部的“初始状态”也可以引起系统的响应。在“连续”系统下,系统的初始状态往往由其内部的“储能元件”所提供,例如电路中电容器可以储藏电场能量,电感线圈可以储存磁场能量等。这些储能元件在开始计算时间时所存储的能量状态就构成了系统的初始状态。如果系统的激励为零,仅由初始状态引起的响应就被称之为该系统的“零输入响应”。一个充好电的电容器通过电阻放电,是系统零输入响应的一个最简单的实例。系统的零输入响应完全由系统本身的特性所决定,与系统的激励无关。当系统是线性的,它的特性可以用线性微分方程表示时,零输入响应的形式是若干个指数函数之和。指数函数的个数等于微分方程的阶数,也就是系统内部所含“独立”储能元件的个数。假定系统的内部不含有电源,那么这种系统就被称为“无源系统”。实际存在的无源系统的零输入响应随着时间的推移而逐渐地衰减为零。
定义
换路后,电路中无独立的激励电源,仅由储能元件的初始储能维持的响应.
也可以表述为,由储能元件的初始储能的作用在电路中产生的响应称为零输入响应(Zero-input response).
零输入响应是系统微分方程齐次解的一部分。
系统的响应除了激励所引起外,系统内部的“初始状态”也可以引起系统的响应。在“连续”系统下,系统的初始状态往往由其内部的“储能元件”所提供,例如电路中电容器可以储藏电场能量,电感线圈可以储存磁场能量等。这些储能元件在开始计算时间时所存储的能量状态就构成了系统的初始状态。如果系统的初始状态为零,仅由激励源引起的响应就被称之为该系统的“零状态响应”。一个原来没有充过电的电容器通过电阻与电源接通,构成充电回路,那么电容器两端的电压或回路中的电流就是系统零状态响应的一个最简单的实例。系统的零状态响应一般分为两部分,它的变化形式分别由系统本身的特性和激励源所决定。当系统是线性的,它的特性可以用线性微分方程表示时,零状态响应的形式是若干个指数函数之和再加上与激励源形式相同的项。前者是对应的齐次微分方程的解,其中指数函数的个数等于微分方程的阶数,也就是系统内部所含“独立”储能元件的个数。后者是非齐次方程的特解。对于实际存在的无源系统而言,零状态响应中的第一部分将随着时间的推移而逐渐地衰减为零,因此往往又把这一部分称之为响应的“暂态分量”或“自由分量”;后者与激励源形式相同的部分则被称之为“稳态分量”或“强制分量”。
零状态响应:电路的储能元器件(电容、电感类元件)无初始储能,仅由外部激励作用而产生的响应。
在一些有初始储能的电路中,为求解方便,也可以假设电路无初始储能,求出其零状态响应,再和电路的零输入响应相加既得电路的全响应。
在求零状态响应时,一般可以先根据电路的元器件特性(电容电压、电感电流等),利用基尔霍夫定律列出电路的关系式,然后转换出电路的微分方程;利用微分方程写出系统的特征方程,利用其特征根从而可以求解出系统的自由响应方程的形式;零状态响应由部分自由响应和强迫响应组成,其自由响应部分与所求得的方程具有相同的形式,再加上所求的特解便得系统的零状态响应形式。可以使用冲激函数系数匹配法求解。
本章小结
习题二
第3章 正弦稳态分析
3-1 正弦量的基本概念
3-2 正弦量的相量表示
3-3 KCL,KVL的相量形式
3-4 RLC元件特性方程的相量形式及相量模型
3-5 阻抗和导纳
3-6 正弦稳态电路的分析计算
3-7 正弦稳态电路的相量图、位形图分析法
3-8 正弦稳态电路的功率
3-9 电路的频率响应
本章小结
习题三
第4章 互感耦合电路
4-1 耦合电感元件
4-2 空芯变压器
4-3 理想变压器
理想变压器是一个端口的电压与另一个端口的电压成正比,且没有功率损耗的一种互易无源二端口网络。它是根据铁心变压器的电气特性抽象出来的一种理想电路元件。
4-4 变压器模型
本章小结
习题四
第5章 正弦稳态三相电路
5-1 三相电路的基本概念
三相电路。三相交流电源指能够提供3个频率相同而相位不同的电压或电流的电源,最常用的是三相交流发电机。三相发电机的各相电压的相位互差120°。它们之间各相电压超前或滞后的次序称为相序。三相电动机在正序电压供电时正转,改为负序电压供电时则反转。因此,使用三相电源时必须注意其相序。一些需要正反转的生产设备可通过改变供电相序来控制三相电动机的正反转。 三相电路是一种特殊的交流电路,由三相电源、三相负载和三相输电线路组成。 世界上电力系统电能生产供电方式大都采用三相制。
5-2 对称三相电路正弦稳态分析
5-3 不对称三相正弦稳态电路分析
5-4 三相电路的功率与测量
本章小结
习题五
第6章 周期性非正弦稳态电路分析
第7章 网络的复频域分析法
附录 中英名词对照
电路理论:时域与频域分析内容简介常见问题
-
本书是根据目前高职高专院校工程造价等专业的教学基本要求编写而成。本书共13章,包括建筑概述,建筑制图与识图的基本知识,基础,墙体,楼板层与地面,楼梯,屋顶,门与窗,变形缝,工业建筑构造,建筑施工图的识...
-
《大设计》无所不在。在会议室和战场上;在工厂车间中也在超市货架上;在自家的汽车和厨房中;在广告牌和食品包装上;甚至还出现在电影道具和电脑图标中。然而,设计却并非只是我们日常生活环境中的一种常见现象,它...
-
本书分为上篇“平面构成”和下篇“色彩构成”两个部分,每一部分的最后章节选编了一些本校历年来学生的优秀作品作为参考,图文并茂、深入浅出。此外,本书最后部分附有构成运用范例及题型练习,可供自考学生参考。本...
电路理论:时域与频域分析内容简介文献

 电路理论基础
电路理论基础
电路理论基础 1:电位是相对的量,其高低正负取决于( )。 回答:参考点 2:不能独立向外电路提供能量, 而是受电路中某个支路的电压或电流 控制的电源叫( )。 回答:受控源 3:振幅、角频率和( )称为正弦量的三要素。 回答:初相 4:并联的负载电阻越多(负载增加),则总电阻越( )。 回答:小 5:任一电路的任一节点上,流入节点电流的代数和等于( )。 回答:零 6:电流的基本单位是( )。 回答:安培 7:与理想电压源( )联的支路对外可以开路等效。 回答:并 8:电气设备只有在( )状态下工作,才最经济合理、安全可靠。 回答:额定 9:通常规定( )电荷运动的方向为电流的实际方向。 回答:正 10:电容元件的电压相位( )电流相位。 回答:滞后 11:两个同频率正弦量之间的相位差等于()之差。 回答:初相 12:电位是相对于( )的电压。 回答:参考点 13:支路电流法原则上适用适

 现代电路理论试题2012
现代电路理论试题2012
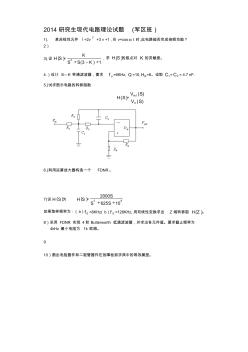
2014研究生现代电路理论试题 (军区班 ) 1). 某非线性元件 i =2v 2 +3 v +1 ,当 v=cos t 时 ,此电路能否完成倍频功能? 2) 3).设 SH = 1)3(2 KSS K ,求 SH 的极点对 K 的灵敏度。 4.)设计 S—K 带通滤波器,要求 pf =6KHz, Q =10, BH =8。设取 1C = 2C = 4.7 nF. 5.)试求图示电路的转移函数 SH = )( )( SV SV in out 6.)利用运算放大器构造一个 FDNR。 7)设 SH 为 SH = 82 10625 2000 SS S 如果取样频率为:(a) Sf =8KHz(b) Sf =128KHz,用双线性变换求出 Z 域转移函 ZH 。 8)采用 FDNR 实现 4 阶 Butterworth 低通滤波器,并求出各元件值。要求截止频率为 4kHz 最小电阻为 1k
集总的线性时不变电路和系统的激励与响应的关系都由常系数线性微分方程来描述。如果施加以正弦形激励,如Asin(ωt 嫓),或指数形激励,如,则其稳态响应一般亦呈同频率的正弦或指数形式。采用复数相量法,只需求解由电路方程所得复数方程组,就可以求得所需的响应。
暂态分析的目的是要研究在电路中施加激励后所出现的响应。对于线性时不变电路和系统,暂态的频域分析的基本思想是将激励展开为许多存在于 -∞tK倍(K是整数)的谐波之和,即为激励的傅里叶级数展开式,所得的响应亦表示为类似的级数形式。在激励是非周期时间函数的情况下,激励的展开式是频率连续分布在-∞ωg(t)=g(t T0) T0≠0性质的信号。满足上式的最小的T0值称为此信号的周期,其频率为f0。
满足狄里赫利条件的周期性时间信号可以用傅里叶级数展开为一系列频率为Kf0(K=整数)的简谐时间函数之和
(1)
式中将式(1)中频率相同的正弦项、余弦项合并,即有
(2)
其中 由(1)、(2)两式可知,周期性时间信号可表示为一系列谐波之和,这些谐波的频率为f0的整倍数,Ck是频率为Kf0的谐波的振幅,φk就是这一谐波的初相角。对一周期性信号可以作出它的各谐波振幅Cn、初相角φn与角频率ω的关系的图像,这种图像分别称为振幅谱和相位谱。图中的周期性矩形脉冲的傅里叶级数展开式是式中 非周期性时间信号的谐波分析 非周期性信号g(t)满足某些条件时,也可以展开为正弦形式的谐波的和。这时,由傅里叶级数的式中令T0→∞,=Δω→dω,可以得到傅里叶积分变换式
(3)
(4)
G(jω)为g(t)的傅里叶变换,g(t)则为G(jω)的傅里叶逆变换,记作
G(jω)=【g(t)】 (5)
g(t)=-1【G(jω)】 (6)
对式(4)可以作这样的解释:g(t)中频率为ω的简谐分量的复振幅以密度G(jω)分布在ω轴上,将这些频率连续分布在(-∞,∞)上的所有谐波相加(积分)即得到g(t)。G(jω)是复数,它的模和幅角都是频率ω的函数。将G(jω)记作
(7)
式中|G(jω)|称作幅频函数,θ(ω)称为相频函数。对于实数值的信号有即幅频函数是ω的偶函数,相频函数是ω的奇函数。
应用 集总的线性系统的输入激励与输出响应的关系可以用一常系数线性微分方程表示
(8)
式中,u0、ui分别表示线性集总系统的输出量和输入量。带上标(K) 的量表示该量的K阶导数,例如等。对于形如ejwt的激励,式(8)所表示的系统的传递函数为
对于任一形式的激励ui(t)作用于此系统所产生的响应u0(t),便可通过将ui作傅里叶变换,得其频谱密度再应用叠加定理分别计算各频率为ω的指数形激励产生的响应,最后将这些不同频率的响应相加使得到u0(t)。它便是系统在ui(t)的作用下产生的零状态响应。这一结果可表示为下面的积分上式就是U0(jω)的傅里叶反变换。在可以用解析的方法得到这一积分的通式的情况下,便可以得到u0(t)的表达式。在许多情况下,是采用数值方法去求上式的数值解。这时要将积分限限制在一有限的范围,并作离散化的处理。由此发展起来的快速傅里叶变换技术,为解决这类问题提供了快速而有效的算法。
法国数学家傅立叶在1807年就写成关于热传导的基本论文《热的传播》,向巴黎科学院呈交,但经拉格朗日、拉普拉斯和勒让德审阅后被科学院拒绝,1811年又提交了经修改的论文,该文获科学院大奖,却未正式发表。傅立叶在论文中推导出著名的热传导方程 ,并在求解该方程时发现解函数可以由三角函数构成的级数形式表示,从而提出任一函数都可以展成三角函数的无穷级数。傅立叶级数(即三角级数)、傅立叶分析等理论均由此创始。
1822年,傅立叶出版了专著《热的解析理论》(Theorieanalytique de la Chaleur ,Didot ,Paris,1822)。这部经典著作将欧拉、伯努利等人在一些特殊情形下应用的三角级数方法发展成内容丰富的一般理论,三角级数后来就以傅立叶的名字命名。傅立叶应用三角级数求解热传导方程,为了处理无穷区域的热传导问题又导出了当前所称的“傅立叶积分”,这一切都极大地推动了偏微分方程边值问题的研究。然而傅立叶的工作意义远不止此,它迫使人们对函数概念作修正、推广,特别是引起了对不连续函数的探讨;三角级数收敛性问题更刺激了集合论的诞生。因此,《热的解析理论》影响了整个19世纪分析严格化的进程。傅立叶1822年成为科学院终身秘书。
根据傅立叶级数的原理,周期函数都可以展开为常数与一组具有共同周期的正弦函数和余弦函数之和。
满足Dirichlet条件的、以T为周期的时间的周期函数f(t),在连续点处,可用下述的三角函数的线性组合(傅里叶级数)来表示:
上式称为f(t)的傅里叶级数,其中,ω=2π/T。
n为整数,n>=0。
n为整数,n>=1。
在间断点处,下式成立:
a0/2为信号f(t)的直流分量。
令
c1为基波幅值,cn为n次谐波的幅值。c1有时也称一次谐波的幅值。a0/2有时也称0次谐波的幅值。
整数n称为谐波次数,也称谐波阶数。
谐波的频率必然也等于基波的频率的整数倍,基波频率3倍的波称之为三次谐波,基波频率5倍的波称之为五次谐波,以此类推。不管几次谐波,他们都是正弦波。
- 相关百科
- 相关知识
- 相关专栏
- 电路的状态变量分析
- 电路设计与制板Protel 99SE基础应用教程
- 电路设计教程——Protel起步与进阶
- 电路(上册)学习指导书
- 电路(第三版)
- 电路(第2版)
- 电路(第5版)学习指导与习题分析
- 电连接
- 电连接器微动磨损分析模型及失效机理的研究
- 电针操作方法
- 电镀厂降温设备
- 电镀后处理
- 电镀实践900例
- 电镀手册
- 电镀液故障处理
- 电镀自动线
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中国工程图学学会成立工程与制造系统集成化分会
- 中国吹制玻璃行业市场前景分析预测年度报告(目录)
- 中国电力井盖行业市场前景分析预测年度报告(目录)
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 中国轨道射灯行业市场前景分析预测年度报告
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 智能磨音频谱分析仪(DF-6811A)使用说明书
- 园林绿化养护精细化管理对河源市园林景观的影响分析
- 应对水源突发污染的城市供水应急处理技术与应用
- 宜兴沈北路二号桥大直径钻孔灌注桩的施工与质量控制
- 招远电视台制作播出系统数字化改造工程的设计与实践
- 正压送风对降低污水厂设备腐蚀的作用与实践(论文)
- 云南郝家河砂岩型铜矿床地质特征与接替资源勘查成果
- 中国民宿消费市场格局分析及十三五发展环境分析报告
- 圆CFRP-钢管混凝土偏压构件荷载-变形关系分析