地震作用
地震作用基本信息
| 中文名 | 地震作用 | 外文名 | earthquake action |
|---|---|---|---|
| 学 科 | 建筑学 | 解 释 | 地运动引起的结构动态作用 |
在结构设计中,为了增强结构抗御地震灾害的能力,早在19世纪就有许多学者研究地震作用的理论。以规范形式肯定下来的先后有静力理论和反应谱理论,此外,在一些重要工程中,往往直接通过地震反应时程分析来改进结构的抗震设计。
地震作用造价信息
20世纪初,日本首先提出水平最大加速度是地震破坏的重要因素。把地面运动最大加速度(塯g)和重力加速度(g)的比值K定义为“水平烈度”,即当房屋重量为G时,水平地震力为KG;可理解为以房屋重量K倍的水平力破坏房屋的静止状态。静力理论曾被很多国家接受,个别国家还在某些结构设计中应用。
强地震引起的地面运动,一般可用强震仪以加速度时程曲线(两个水平向、一个竖向)的形式记录,其中对结构产生作用的最重要特征是加速度最大值(也称加速度峰值)、频率成分和持续时间。从图1 a、b可知,两个记录分别具有不同的频率成分(波形A、波形B),其各自的主要频率也称卓越频率(其倒数为卓越周期);土愈软则卓越周期愈长,并随震中距而异。持续时间从几秒至几十秒,随震级、震中距以及地表软土覆盖层厚度而变化。地震时,在结构的某些部位装上传感器把信号记录下来,可得到地震反应的物理量:如加速度、速度、位移和应变等,用以定量估计地震作用,以便在工程结构抗震设计中应用。
地震作用常见问题
-
结构设计规范一般都要求对结构分析的结果做判断,一方面是基于计算模型的检查,保证计算结果的正确合理性;另一方面是对规范要求的结构设计控制指标做概念性判断。以下这些内容整理于网络,希望大家一起分享自己的经...
-
地震作用计算是结构抗震设计首先要解决的问题。我国自89抗震规范开始采用按多遇地震(小震)计算地震作用。国际上主要抗震国家和我国78抗震规范都采用按设防烈度地震(中震)计算地震作用。随着抗震规范在修订、...
-
选择“总刚”计算; 计算位移时点“刚性楼板假定”; 计算配筋时不点“刚性楼板假定”――配筋以这个结果为根据
在地震的地面运动作用下,分析结构反应的过程称地震反应分析。分析时常把研究的结构看成一个“系统”,把地面运动看成对该系统的输入,系统的输出便是地震反应。以最简单的单自由度弹性体系作为该系统的一例,其质点在地震动作用下的运动方程式为m【塯(t) 塯g(t)】 c凧(t) kyx(t)=0式中m为质量;塯g为地面运动加速度(即输入);塯、凧及x为质点相对于基底的加速度、 速度和位移(即反应);【塯(t) 塯g(t)】 为绝对加速度;c为阻尼系数;ky为刚度。m【塯(t) 塯g(t)】为质点运动的惯性力。 c凧(t)为阻尼力(阻尼愈大反应愈小)。kyx(t)为恢复力;是质点在地震作用下力图恢复到原来位置的力。在无阻尼自由振动中,质量m和刚度ky决定体系的自振频率(或周期)。在相同的地面运动下,不同自振频率体系的质点反应不一样;反之,把不同地面运动输入同一体系的反应也不一样。因此,地震作用不同于重力等其他作用,它和地面运动特性以及结构本身的动力特性(频率、阻尼)有关。在地震反应分析中,如果把地面运动作为确定的过程进行分析便是确定性的地震反应分析。由于地面运动带有随机性质,如果把地面运动作为随机过程分析便是概率性的地震反应分析。
考虑地面运动加速度和结构动力特性的计算理论。其中有反应谱理论和地震反应时程分析。
地震作用反应谱理论
20世纪30年代初期,美国首先提出了反应谱概念。1943年M.A.毕奥发表了以海伦娜等地地震为例的几条加速度谱曲线, 用扭摆模拟方法绘制,横坐标为单质点体系的自振周期,纵坐标为体系质点的最大加速度值,这就是加速度反应谱。显然,输入相同的地震记录,最大加速度值随体系自振周期的改变而变化。如果把数量足够多的实际地面运动记录作为输入,可以得到多条类似的曲线,然后经过统计分析可以确定一条或数条随场地土质条件变化的标准反应谱曲线以供设计应用,这就是反应谱理论。自50年代起,美国和苏联开始采用反应谱理论,大多数国家的规范都采用了。中国自50年代中期开始在抗震设计中采用了反应谱理论。70年代的谱曲线形状如图2所示,图2中α为地震影响系数,它是最大绝对加速度与重力加速度的比值,当设计烈度为 7度、8度、9度时,α分别为0.23、0.45、0.90;Ⅰ类场地为坚硬的土,Ⅲ类场地为较软弱土,Ⅱ类场地土介于Ⅰ、Ⅲ之间。在抗震设计中,从静力理论过渡到反应谱理论是一个质的变化。反应谱曲线不仅可以直接提供单自由度体系的弹性地震力,对于多自由度体系,也可以通过振型分解把结构化为若干个单自由度以便利用同一谱曲线。
地震作用地震反应时程分析
在抗震设计中,有时还要直接进行确定性的地震反应时程分析。在进行分析时,除需选择合适的地震记录外,还要确定结构的力学模型、结构构件的恢复力特性和计算方法。
在建筑结构中,可以根据实际情况把结构简化为单自由度体系或多自由度体系等力学计算模型。结构或结构构件的恢复力与位移关系主要通过试验获得。恢复力和位移的关系可以分为弹性的和非弹性的。为了便于计算,非弹性的恢复力P和位移x关系可以简化成折线的弹塑性模型。按照弹性恢复力关系求得的反应便是确定性的弹性地震反映;按照弹塑性模型求得的反应,则是确定性的弹塑性地震反应。由于地面运动加速度塯g(t)不能用数字式表达,因而只能把加速度-时间曲线按很小的时段划分,逐段对运动方程式用电子计算机进行直接积分,从而求得各个时刻的地震反应。图3为自振周期较短的某砖混房屋输入不同波形的地面运动加速度记录后的弹性反应。很明显,由于波形A的卓越周期长于波形B,因而波形A的反应小于波形B。显然结构自振周期愈接近地面运动卓越周期,其反应也愈强烈。这样,就需要输入若干个与结构物所在场地土条件相近的地表记录求算最大反应的包络图,找出结构的薄弱之处,以便加强由于地震作用引起房屋损坏的部位。又如对于已经产生震害的结构,地震反应时程分析的结果也能较好地揭示地震震害发生的位置和程度。此外,对于某些不满足抗震鉴定要求的待加固结构,可通过地震反应时程分析作出进一步鉴定和寻求最佳的加固方案。
在地震反应时程分析中,对刚度中心与质量中心不重合的结构,要考虑水平地面运动输入引起的结构扭转;对某些高耸结构,特别是质量分布不均并位于震中区附近的高耸结构,要考虑竖向地面运动的作用;对较长的结构还要考虑沿结构不同长度处的地面影响。2100433B
地震作用文献

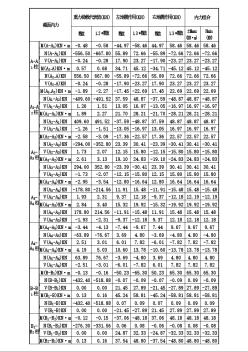 地震作用组合
地震作用组合
截面内力 重力荷载代表值(KN) 左地震作用(KN) 右地震作用(KN) 内力组合 数值 1.2*数值 数值 1.3*数值 数值 1.3*数值 ±Mmax (KN·m) Nmin (KN) A-A1柱 柱下端 M(A-A1)KN·m -0.48 -0.58 -44.97 -58.46 44.97 58.46 58.46 58.46 N(A-A1)KN -556.50 -667.80 55.89 72.66 -55.89 -72.66 72.66 -72.66 V(A-A1)KN -0.24 -0.28 17.90 23.27 -17.90 -23.27 23.27 -23.27 柱上端 M(A1-A)KN·m

 多维地震作用下偏心结构地震反应分析
多维地震作用下偏心结构地震反应分析
文章首先建立了多维地震动作用下非对称结构动力反应分析模型;其次,结合上述内容构建了相应的动力方程;最后,选取双向偏心钢筋混凝土框架结构进行多维地震动作用下的时程反应分析,得到了结构的位移速度反应,并分别考虑单向地震输入、双向地震输入以及扭转加双向地震输入下的结构位移响应,以得出结构多维输入对结构反应的影响,指出了进行多维地震反应分析的必要性.
地震作用:
能引起结构内力、变形等反应的各种因素直接作用:各种荷载:如重力、风载、土压力等间接作用:各种非荷载作用:如温度、基础沉降、地震等等效地震荷载:工程上,可将地震作用等效为某种形式的荷载作用。
以上内容均根据学员实际工作中遇到的问题整理而成,供参考,如有问题请及时沟通、指正。
在地震作用下结构产生的内力(剪力、弯矩、轴向力、扭矩等)或变形(线位移、角位移)等的现象。
结构顶点位移计算,(荷载自上向下传递累加,水平的地震作用有柱子的总体抗侧移刚度来承担)由此计算出最大的层间侧移值,UT。
根据公式计算结构的自振周期T1。
再根据计算的建筑的总的重力荷载代表值之和以及结构类型等因素求解F EK。
再根据位置和本层的荷载代表值计算本层标高处的地震剪力。
(理解分析:水平地震作用对建筑的破坏是由于柱子的抗侧移刚度不足以抵御地震剪切力的作用,地震的剪切力的由来与重力荷载代表值,以及简化的重力荷载所处的位置。详细的相关性联系可以参考一般的参考书。)
- 相关百科
- 相关知识
- 相关专栏
- 地震动孔隙水压力
- 地震动水压力
- 地震勘探施工工日劳动定额
- 地震勘探钻机作业安全规程
- 地震区的场地与地基基础 (平装)
- 地震及高水压下混凝土坝断裂行为的扩展有限元法研究
- 地震台站建设规范重力台站
- 地震台网设计技术要求重力观测网
- 地震地下流体观测方法井水和泉水温度观测
- 地震地质建模
- 地震地质灾害配电应急抢修培训教材
- 地震地质灾害
- 地震地面运动及其人工合成
- 地震场地影响观测台阵设备
- 地震安全性评价工程技术人员
- 地震工程与特殊条件下的岩土工程
- 在大荷载作用下人工挖孔灌注桩桩基承台的设计与施工
- 园林植物在城市景观设计中的作用
- 在面内压力作用下点腐蚀低碳钢板的非线性有限元分析
- 在耐热铬铝合金改性处理中钒渣的冶金物化条件及作用
- 有建筑物存在的软土地基液化模拟地震振动台试验
- 政府引导 农民自主 海南农居地震安全工程大放异彩
- 再力花地下部水浸提液对几种常见水生植物的化感作用
- 园林绿化对城市建设与发展的促进作用
- 公路桥梁箱梁悬臂施工中预应力作用及剪力滞效应
- 关于工程场地地震安全性评价中设计地震动反应谱讨论
- 改性聚丙烯纤维对混凝土裂缝抑制作用与应用进展
- 关于强化经济责任审计在反腐倡廉中监督作用调研报告
- 关于不规则隔震结构建筑方案在地震作用下讨论
- 改性聚丙烯纤维砂浆在清水混凝土罩面早期开裂时作用
- 构建生态城市进程中园林绿化管理作用分析及对策
- 公路钢护栏圆形立柱与土壤基础相互作用力学特性