等额分付终值
等额分付终值基本信息
| 中文名 | 等额分付终值 | 定 义 | 一定时期内,间隔相等时间支付固定的金额(通常叫做分次付款)、各期分次款及由这些分次款复利累积的总和 |
|---|
某企业每年年末在单独账户中存入人民币10万元,以备5年后设备更新之需,如果存款利率为10%,第5年年末该企业在该账户中可支配的资金是多少"para" label-module="para">
已知A=10,i=10%,n=5
则:F=A(F/A,i,n)
=10×(F/A,10%,5)
=10×6.105
=61.05(万元)
等额分付终值造价信息
1 张静.企业项目管理咨询与诊断.中国经济出版社,2003年06月第1版.
2 武献华,宋维佳,屈哲.工程经济学.东北财经大学出版社,2007.4. 2100433B
如图1所示,从第1年年末到第n年年末,有一等额的现金流系列,每年的流出金额均为A,在考虑资金时间价值的情况下,如果n年内系统的总现金流出等于总现金流入,那么第n年年末的现金流入F应与等额现金流出序列等值。F即为等额支付系列的终值。
在已知等额年值A,利率i,计息周期数n的条件下,可以把它视为n个一次支付的组合,然后利用整付终值公式分别求出各次支付的终值,再求和。
F = A(1 i)n − 1 A(1 i)n − 2 ... A(1 i)1 A(1 i)0
=A[1 (1 i) ... (1 i)n − 2 (1 i)n − 1]
上式方括号忠是一个公比为(1 i)的等比级数,其前n项和为:
F=A(F/A,i,n)
等额分付终值系数等同于年金终值系数(Future value of an annuity factor)=F/A=(F/A,i,n)
等额分付终值常见问题
-
某项目建设期2年,建设期内每年年初贷款1000万元。年初贷款相当于上一年的年终贷款,第一个的年初贷款相当于建设期的上一年年终贷款,建设期的第二年贷款相当于建设期的第一年年终贷款,用1000×(F/A,...
-
f:future value终值p:present walue 现值终值=现值*复利终值系数现值=终值*复利现值系数这是计算资金时间价值的公式,对应系数可以通过查复利现值系数表和福利终值系数表找出。...
-
年金终值是指等额年金复利折算到未来某一时间点的价值。年金现值是等额年金以一定的折现率折算到当前的价值。
整付终值
整付现值
等额分付现值
等额分付偿债基金
等额分付资本回收
等额分付终值文献

 财务管理系数表、年金现值、终值、复利现值、终值
财务管理系数表、年金现值、终值、复利现值、终值
附表一 复利终值系数表 期数 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 1 1.0100 1.0200 1.0300 1.0400 1.0500 1.0600 1.0700 1.0800 1.0900 1.1000 2 1.0201 1.0404 1.0609 1.0816 1.1025 1.1236 1.1449 1.1664 1.1881 1.2100 3 1.0303 1.0612 1.0927 1.1249 1.1576 1.1910 1.2250 1.2597 1.2950 1.3310 4 1.0406 1.0824 1.1255 1.1699 1.2155 1.2625 1.3108 1.3605 1.4116 1.4641 5 1.0510 1.1041 1.1593 1.2167 1.2763 1.3382 1.4026 1.4693 1.5386 1

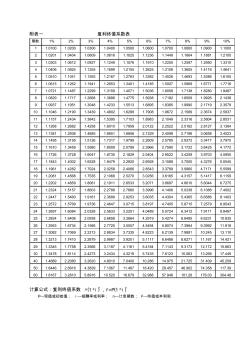 财务管理系数表:复利终值-复利现值-年金终值-年金现值
财务管理系数表:复利终值-复利现值-年金终值-年金现值
附表一 复利终值系数表 期数 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 1 1.0100 1.0200 1.0300 1.0400 1.0500 1.0600 1.0700 1.0800 1.0900 1.1000 2 1.0201 1.0404 1.0609 1.0816 1.1025 1.1236 1.1449 1.1664 1.1881 1.2100 3 1.0303 1.0612 1.0927 1.1249 1.1576 1.1910 1.2250 1.2597 1.2950 1.3310 4 1.0406 1.0824 1.1255 1.1699 1.2155 1.2625 1.3108 1.3605 1.4116 1.4641 5 1.0510 1.1041 1.1593 1.2167 1.2763 1.3382 1.4026 1.4693 1.5386 1
等额支付系列的终值与现值的计算
1、等额支付系列的现金流量
间隔相等周期连续发生的现金流量称为等额支付系列,若间隔周期为一年,则为等额年金。
2、等额支付终值公式(已知A、i、n,求F)
在资金等值计算时我们一般可以绘制现金流量图。发生在一到四年内每年末的年值的通过等值计算到第四年末的终值可逐年进行折算。
当等额支付系列发生次数逐渐增加时,逐年折现会越来越麻烦,而且考试时间也不允许,实际我们分析规律,当需要将1到n年内每年末发生等额值A等级计算到n年末时:
这个公式就是等额支付系列终值公式,对于发生在n年内每末的等额年值折算到n年末(和最后一个A同时刻)的终值时可以直接套用公示。但对于复杂情况,仅仅套公式是不行的,需要进行多次换算。
等额本金贷款,相对于等额本息贷款,它采用了简单的方式来计算利息,只有本金产生利息(而等额本息贷款,本金和利息都需要产生利息),这样,在贷款条件相同的情况下,采用等额本金贷款,明显要比等额本息贷款花费更少的利息。
等额本金贷款计算公式:
每月还款金额= (贷款本金/ 还款月数) (本金 — 已归还本金累计额)×每月利率
从公式可以看出,等额本金贷款计算出的每期还款金额都不同,从还款前期到后期,金额都是逐渐减少的,而等额本息贷款计算出的还款金额,每期都相等。2100433B
等额本息贷款采用的是复合利率计算。在每期还款的结算时刻,剩余本金所产生的利息要和剩余的本金(贷款余额)一起被计息,也就是说未付的利息也要计息。在国外,它是公认的适合放贷人利益的贷款方式。
每月的还款额相同,从本质上来说是本金所占比例逐月递增,利息所占比例逐月递减,月还款数不变,即在月供“本金与利息”的分配比例中,前半段时期所还的利息比例大、本金比例小。还款期限过半后逐步转为本金比例大、利息比例小。
等额本金贷款采用的是简单利率方式计算利息。在每期还款的结算时刻,它只对剩余的本金(贷款余额)计息,也就是说未支付的贷款利息不与未支付的贷款余额一起作利息计算,而只有本金才作利息计算。
每月的还款额减少,呈现逐月递减的状态;它是将贷款本金按还款的总月数均分,再加上上期剩余本金的利息,这样就形成月还款额,所以等额本金法第一个月的还款额最多 ,然后逐月减少,越还越少。
二者相比,在贷款期限、金额和利率相同的情况下,在还款初期,等额本金还款方式每月归还的金额要大于等额本息。但按照整个还款期计算,等额本金还款方式会节省贷款利息的支出。
等额本息的优点是每月还款额相同,方便安排收支,适合经济条件不允许前期还款投入过大,收入处于较稳定状态的借款人。缺点是需要付出更多的利息。不过前期所还的金额大部分为利息,还款年限过半后本金的比例才增加,不合适提前还款。
等额本金的优点是相对于等额本息的总利息较少。还款金额每月递减,后期越还越轻松。且由于前期偿还的本金比例较大,利息比例较少,所以很适合提前还款。缺点是前期还款压力较大,需要有一定经济基础,能承担前期较大还款压力。
等额本金和等额本息哪个适合提前还款?
等额本金前期还的本金多、利息支出少,显然更适合提前还款。
等额本息前期每个月还款额度中,本金比例少,利息比例较多,不适合提前还款。
我该如何选择等额本息和等额本金?
贷款总额越少(5~20万),年限越短(5-10年),两者区别不大,一般总利息差距在0.1-1万元以内。
贷款总额越高(100万以上),年限越长(15年以上),两者差距较大,等额本息比等额本金多支付的利息将超过10万元以上。
制定适合自己的还款方式,量力而行。若对数字没有直观的理解,可用房贷计算器事先计算一下等额本息和等额本金这两种方式的差别。
- 相关百科
- 相关知识
- 相关专栏
- 等额本息
- 等额本金贷款
- 等额还款抵押贷款
- 等高线地图
- 筏板
- 筐篓
- 筐篚
- 筑地建设有限公司
- 筑建
- 筑版
- 筑艺匠
- 筑造
- 筑龙一六八网络科技(深圳)有限公司
- 筑龙建材科技(深圳)有限责任公司
- 筒单级数反应
- 筒子纱圈位移角
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 电气工程及其自动化特色专业建设探索
- 分形DGS单元结构设计及其在微带电路中的应用
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 预制砌块(砖、石)挡土墙工程砌体施工安全技术交底
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中华华丹雨、污水管道沟槽开挖专项施工方案教学教材
- 中国工程图学学会成立工程与制造系统集成化分会
- 中国吹制玻璃行业市场前景分析预测年度报告(目录)
- 可替代现有隔热保温材料的新型材料
- 医院病房楼工程施工装饰装修工程施工控制
- 在生活中构筑自然——河南天旺园林工程有限公司剪影
- 中国机械工程学会授予材料热处理工程师资格人员名单