点到直线距离
点到直线距离基本信息
| 中文名 | 点到直线距离 | 外文名 | Distance from a point to a line |
|---|---|---|---|
| 主 体 | 连接直线外一点与直线上各点之和 | 特 点 | 垂线段最短 |
| 斜 率 | -A/B | ||
点到直线距离造价信息
点到直线距离常见问题
-
解:设点A坐标(x1,y1)直线方程:ax+by+c=0A到直线的距离=|ax1+by1+c|÷√(a²+b²)
-
1、点到直线的距离点P(x0,y0)到直线 Ax+By+C=0的距离可表示为:d=|Ax0+By0+C|/√(A^2+B^2)
-
正常来讲 柱边个墙边应该是平的 把墙用单对齐的功能对齐柱边就好了 如果你的墙是这样的 一定要测距离的话 只能在外墙边增加一根辅助轴线 可以解决你的问题
点到直线距离文献

 点到平面的距离(1)
点到平面的距离(1)
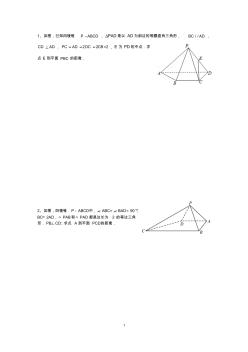
1 1、如图,已知四棱锥 P ABCD , PAD是以 AD为斜边的等腰直角三角形, / /BC AD , CD AD , 2 2 =2PC AD DC CB , E 为 PD的中点.求 点 E 到平面 PBC 的距离 . 2、如图,四棱锥 P-ABCD中,∠ ABC=∠ BAD= 90°, BC= 2AD,△ PAB和△ PAD都是边长为 2 的等边三角 形. PB⊥CD;求点 A到平面 PCD的距离. 2 3 、 如 图 , 在 四 棱 锥 P ABCD 中 , / /C D P A D A BCD平面 , 4 4, ,CD AD AB AC PA且 M 是线段 CP上一点 / / 1 1 = = 4 2 PM PC AP AD P DMB A平求 面且 , 证 , M ABCD并求点 到平面 的距离 4、如图,四棱锥 P ABCD中,底面 ABCD 为平行四边形, 60DAB

 点到平面的距离(文科)
点到平面的距离(文科)
点到平面的距离 (文科数学 ) 1.【2018 年全国卷 II 文】如图,在三棱锥 中, , , 为 的中点. (1)证明: 平面 ; (2)若点 在棱 上,且 ,求点 到平面 的距离. 【答案】(1)见解析( 2) . (2)作 CH⊥OM,垂足为 H.又由( 1)可得 OP⊥CH,所以 CH⊥平面 POM.故 CH的长 F E D C BA 为点 C到平面 POM 的距离.由题设可知 OC= =2,CM = = ,∠ ACB=45°.所以 OM= ,CH= = . 所以点 C到平面 POM 的距离为 . 点睛:立体几何解答题在高考中难度低于解析几何, 属于易得分题, 第一问多以线面的证明 为主,解题的核心是能将问题转化为线线关系的证明; 本题第二问可以通过作出点到平面的 距离线段求解,也可利用等体积法解决 . 2. (2005年福建高考题)如图 1,直二面角 EABD 中,四边形 A
高中 数学
1.四.解析几何初步/1.直线与直线的方程
2.四.解析几何初步/1.直线与直线的方程/点到直线距离公式
直线解析式点到直线距离
点
直线解析式两平行线之间距离
若两平行直线的方程分别为:
角度处理:两直线夹角、直线与Y轴夹角、直线与X轴夹角
点线处理:两直线交点、交点到直线距离、交点到交点距离、交点到圆心距离、交点到点距离
圆处理:圆心距离、圆心到直线的距离、交点到圆心的距离、直线到切点的距离
线处理:直线度、凸度、LG凸度、对数曲线
- 相关百科
- 相关知识
- 相关专栏
- 园林细部设计与构造图集4
- 红花槭
- 珍珠绣线菊
- 中国注塑机网
- 麻叶绣线菊
- 有机覆盖物
- 点测光
- 景观工程细部CAD图集:坐凳
- 菱叶绣线菊
- 思源广场
- 李叶绣线菊
- GBN-501光学光敏胶
- 凝固点
- 绿化施工员
- 新疆草原监理站
- 黄芦木
- 引绰济辽工程远距离输水隧洞TBM施工三维数值模拟
- 医用直线加速器机房升级改造中的主要问题及解决方案
- MJS工法在砂卵石地层盾构近距离下穿运营地铁隧道的应用
- 110、220kV空气间隙线路避雷器直线塔安装方式
- 新疆北疆长距离干渠BSP段湿陷性黄土地基处理措施分析
- 土压平衡盾构长距离穿越群房基础时的微扰动施工技术研究
- 多刀盘土压平衡顶管机在长距离三维急曲线顶管施工中的应用
- AFC数据的新建轨道交通系统出行距离分布特性研究
- 市政给排水施工中长距离顶管施工技术及实施要点
- 复杂条件下暗挖隧道近距离穿越施工既有桥梁的影响研究
- 大体积泵送混凝土在高温、远距离运输条件下施工实例
- 大气环境防护距离与卫生防护距离确定技术方法对比
- Excel回归直线分析法在施工机械成本管理中应用
- 城市轨道交通特定安全防护距离下的极限进站方案
- 大华桥水电站砂石加工系统长距离胶带机施工技术
- 光纤组束激光对可见光硅CCD的有效干扰距离分析
