电磁场与传输线的相互作用
电磁场与传输线的相互作用基本信息
| 书 名 | 电磁场与传输线的相互作用 | 作 者 | 法哈德·拉奇迪 |
|---|---|---|---|
| 出版时间 | 2013年3月 | 页 数 | 208 页 |
| 定 价 | 48 元 | ISBN | 9787302305934 |
| 副标题 | 从经典理论到高频辐射效应 | ||
第一部分 经典传输线理论
第1章 电报员方程和场—传输线耦合作用方程的推导
1.1 传输线(TL)近似
1.2 良纯导体地面上的单根导线
1.2.1 Taylor,Satterwhite&Harrison模型
1.2.2 Agrawal,Price&Gurbaxani模型
1.2.3 Rachidi模型
1.3 不同电磁场分量的贡献
1.4 包含损耗
1.5 多导体传输线的情形
1.6 耦合方程的时域表征
1.7 频域解
1.7.1 格林函数
1.7.2 BLT方程
1.8 时域解
1.9 小结
参考文献
第2章 架空多导体传输线的浪涌传播和串扰
2.1 引言
2.2 MTL系统的电报员或传输线方程
2.2.1 导线内部阻抗的表示
2.2.2 有限电导率地面上的导线外部阻抗和导纳
2.2.3 单位长传输线的完整表述和每个传输线参数的灵敏度
2.2.4 架空导线的时域传输线方程
2.3 传输线方程的时域数值解
2.3.1 时域有限差分方法
2.3.2 MTL系统的频域解
2.3.3 直接频域解和FDTD方法的比较
2.4 系统中的串扰
2.4.1 弱耦合条件下电小尺寸导线的串扰
2.4.2 强耦合条件下的串扰
2.5 小结
致谢
参考文献
第3章 地下多导体传输线的浪涌传播
3.1 引言
3.2 埋地导线的电报员或传输线方程
3.2.1 埋地导线的地阻抗
3.2.2 埋地导线的地导纳
3.3 埋地导线传输线近似的限制条件
3.4 通过电缆屏蔽层对电缆芯线的耦合
3.4.1一般性的双屏蔽三芯电缆
3.4.2 RG—58电缆的例子
3.4.3 耦合现象中屏蔽层厚度的影响
3.4.4 求取电缆内导体电感和电容矩阵元素的一种简便测量方法
3.5 其他一些导线几何位置的地阻抗例子
3.5.1地表导线的阻抗
3.5.2架空导线和地下导线之间的互阻抗
3.6一些例子
3.6.1 裸导线和绝缘导线上脉冲传播的时域仿真
3.6.2 一个实际的串扰问题
3.7 小结
致谢
参考文献
第二部分改进的传输线理论
第4章 对传输线的高频电磁耦合:传输线近似的电动力学修正
4.1 引言
4.2 高频电磁场对良导体地面上架空直导线的耦合
4.2.1 对有限长细导线的类TL形式的电场积分方程(EFIE)推导
4.2.2 频域耦合方程的迭代解
4.2.3 平面波对无限长导线的耦合:确定解和迭代解
4.2.4 对半无限长开路导线反射系数的修正
4.2.5 有限长直导线耦合方程的时域迭代解
4.2.6 有限长导线求解步骤收敛性讨论
4.3 高频电流波在导线弯曲段的传播
4.3.1 问题描述
4.3.2 导线弯曲段的描述:电场积分方程的推导
4.3.3 电场积分方程的迭代解
4.3.4 所提出方法的验证
4.3.5 辐射功率
4.4 小结
参考文献
第5章 高频电磁场对带负载的非均匀长导线的耦合:渐近方法
5.1 简介
5.2 高频电磁场对带负载长导线的耦合
5.2.1 渐近方法
5.2.2 本章提出的导线渐近区感应电流三项表达式计算方法的精确度
5.2.3 应用:带负载的长导线对外界平面波的响应
5.3 非均匀传输线的渐近方法
5.4 小结
附录A 用系数I1和I2来计算系数R ,R_,C ,C_
附录B 用第4章给出的迭代方法推导半无限长开路导线的系数C 和C_的解析表达式
附录C 含有集总阻抗导线的渐近区域里感应电流的解析表达式
参考文献
第6章 常规高速互连线和金属碳纳米管互连线的传输线模型
6.1 引言及历史背景
6.2 广义积分公式和传输线模型的推导
6.2.1 积分公式
6.2.2 传输线方程
6.3 常规导线的传输线模型
6.3.1 圆柱形对线
6.3.2 耦合微带线
6.4 CNT互连线的传输线模型
6.4.1 CNT流体模型
6.4.2 地平面之上SWCNT的传输线模型
6.5 例子及应用
6.5.1 有限长度和临近效应
6.5.2 高频损耗
6.5.3 高频串扰和模式转换
6.5.4 CNT和铜互连线在纳米电子学应用中的比较
6.6 小结
致谢
参考文献
第7章 电磁场对埋地导线的耦合:频域和时域分析
7.1 引言
7.2 频域方法
7.2.1 频域公式方法
7.2.2 微积分方程的数值解
7.2.3 瞬态响应的计算
7.2.4 数值结果
7.3 时域方法
7.3.1 时域公式
7.3.2 时域能量量度(Time domain energy meastlres)
7.3.3 时域数值解步骤
7.3.4 利用简化反射/传输系数的另一种时域求解公式
7.3.5 算例2100433B
电磁场与传输线的相互作用造价信息
《电磁场与传输线的相互作用(从经典理论到高频辐射效应)(精)》编著者(瑞士)法哈德.拉奇迪(FarhadRachidi)、(俄罗斯)谢尔盖?特卡琴科(SergeyTkachenko)。
《电磁场与传输线的相互作用:从经典理论到高频辐射效应》内容包括了经典的传输线理论,以及最近的研究新进展,特别是在考虑高频效应方面的内容,可供对传输线理论和电磁场与传输线相互作用感兴趣的研究生、理论研究工作者和工程师参考使用。
《电磁场与传输线的相互作用(从经典理论到高频辐射效应)(精)》内容有七章,包括两个主要部分,第一部分给出了经典的传输线理论知识和不同的场一线耦合模型;第二部分介绍了为包含高频辐射效应而发展的几种广义传输线理论方法。
电磁场与传输线的相互作用常见问题
-
体对来自导线、电缆、元部件、电路或系统等外部的干扰电磁波和内部电磁波均起着吸收能量(涡流损耗)、反射能量(电磁波在体上的界面反射)和抵消能量(电磁感应在层上产生反向电磁场,可抵消部分干扰电磁波)的作用...
-
5-10块钱一条吧。。 有一种比较贵的 质量比较好!叫CA77187-1501 还有一款比较便宜 质量比...
-
深圳市昌盛达电脑有限公司供应DVI 双24针接口线 DVI连接线 DVI线 DVI传输线 DVI数据线.品牌/型号:CSD/40类型:DVI线接口类型:DVI型号:40线材材质:铜品牌:CSD.价格:...
电磁场与传输线的相互作用文献

 电磁场对镁合金熔体的净化作用
电磁场对镁合金熔体的净化作用
对无磁场与静磁场作用下AZ61镁合金的凝固组织进行了研究。结果发现,静磁场作用下的镁合金凝固组织中夹杂物明显减少或呈球状分布,说明静磁场对AZ61镁合金熔体具有净化的作用,因此,静磁场可以改善镁合金的性能。
电子与固体的相互作用
入射电子的散射、反射、吸收和衍射,是电子显微镜和电子衍射仪的物理基础。利用电子轰击下的次级发射(包括俄歇电子发射)现象,人们研制出扫描电镜、俄歇电子能谱仪和电子倍增器。在电子轰击下使固体内部和表面力键断裂及等离子激光的激发可以用电子能量损失谱来分析,而其中晶格振动加剧部分则可用表面声子谱来研究。
在电子轰击下可以产生轫致辐射和特征 X射线辐射,X 射线管和电子探针分析仪即利用这些现象。如果被轰击的固体是发光材料(例如荧光粉),则辐射可见光或不可见射线。黑白和彩色显像管、示波管和其他一些显示器件,就是利用这种现象来显示图像、图形、字符的。电子束轰击所产生的热效应,可以用于热电子发射、电子束退火、电子束焊接、电子束切割和电子束熔炼。
电子轰击可以诱发物理和化学反应,例如可以使表面原子或分子脱附(电子诱导脱附)或使固体表面组分分解或聚合,也可能由此而产生某种元素的表面污染或沉积。电子束轰击可以使近表面层产生反应,例如可以用来使某些薄膜着色或使曝光胶曝光。
借助自旋极化电子束与表面相互作用可以获得更多的信息。
光子与固体的相互作用
各种波长的光束与固体相互作用时,入射光子本身可能被反射、吸收和散射,也可能产生衍射和偏振。这类现象主要用于分析和测量仪器,例如X射线衍射仪和椭圆偏振仪等。光束的热效应可以用于加工(例如激光退火、激光焊接、激光打孔),还可用于激光武器。
在光子的作用下,固体表面和内部会产生各种激发和驰豫过程,例如产生光电子、 俄歇电子、 光电导等。这些现象已广泛应用于真空电子器件、固态电子器件以及表面分析仪器中,例如像增强管与变像管、光电管与光电倍增管、光电摄像管、红外探测器、紫外光电子能谱仪、X射线光电子能谱仪等。
光子可能诱导固体表面的吸附物脱附或分解,导致吸附或强化气相沉积,或使表面和内部产生光合成以及其他化学反应。这些现象可用于微电子技术中的光刻和X射线光刻等。
离子与固体的相互作用 离子与固体相互作用的现象和过程比较复杂。入射离子可能产生背散射或与表面原子作用而散射(低能离子散射谱),也可能进入固体内部而形成离子注入。
在离子束轰击下,能够从表面溅射出大量的原子、分子、原子团和各种正、负离子。溅射现象可用于刻蚀、薄膜减厚和薄膜的溅射沉积等。溅射出来的次级正、负离子的发射过程包含着电离、激发、中和、结合等一系列物理化学过程。因此,入射离子的化学性质是控制次级离子发射的重要因素。次级离子发射用于动态和静态次级离子质谱仪,后者破坏性极小。
利用离子激发次级电子和 X射线的现象的分析仪器有离子激发俄歇谱仪、离子激发 X射线分析仪以及离子中和谱仪。
离子轰击固体时,往往对固体表面和邻近表面层的成分和结构产生改性作用,例如择优溅射、嵌埋效应、诱导扩散和反应、离子注入等,都会改变近表面层的成分和组态,而级联碰撞则会改变表面形貌和晶格取向,甚至导致无序化;也会在较深层造成大量晶格缺陷。因此应注意控制入射离子束流的能量和密度,以减小它的影响(见真空表面分析技术、真空镀膜、离子表面处理、电子束加工、电子束与离子束微细加工、电子显微镜)。
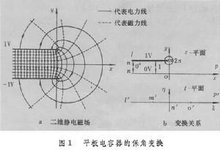
电磁场的保角变换正文
数学上规定复平面和复平面之间的变换=()是导数′()厵0的各点处是保角变换,它是求解二维电磁场问题的一种有力工具。例如两个平行的柱形电极,当长度远大于间距从而可以忽略柱体的末端效应时,就可近似为二维问题。保角变换可应用于:静电、静磁问题,包括传输线(即横电磁场)问题;具有复杂边界的导波系统问题;以及电磁场的反演问题。
静电、静磁问题的应用甚广,在电源或磁源以外的区域,二维问题的电场强度或磁场强度等于某一静势函数的梯度,后者满足二维拉普拉斯方程,其解称为(圆)调和函数,记为(,),则
设复变数=+j,则根据已知的(,),总可以找到另一个调和函数=(,),构成解析函数
ω(z)=u+jv
z=x+jy
称和为共轭函数,为复势函数。可以证明也满足二维拉普拉斯方程并且在复平面上的等值线是两簇互相正交的曲线。若选其中的一簇为等势线,则另一簇就代表力线(电力线、磁力线),相应地称这两簇曲线所对应的函数为势函数和流函数(通量函数)。
电磁场的保角变换 若能找到两个共轭函数,其中一个函数的等值线恰好和所研究的电极边界重合,则另一个函数的等值线即代表由电极发出的电力线。因而,根据电力线的流函数就可以计算出电极表面所带的电荷量,从而可以计算场分布和电容量等。例如平板电容器二维边缘场的分析(图1a)。设两极板的电位分别为±1伏,间距为2(长度单位),置于-平面中(=+j),根据对称性,只需分析上半平面(>0)的场。利用解析函数
的保角变换(=+j),使-平面上由点、、连成的多角形变换成以点′、′、′连线为界的上半-平面(图1b)。已知后者的复势函数为
故平板电容器的复势函数满足关系式
据此可得出在-平面内的等势线(=常数)和电力线(=常数)的曲线方程。
某些边界形状较复杂的导波系统,经保角变换可变换成一个较易处理的简单边界形状。例如利用波导的电磁场解描述沟槽形波导(图2)的电磁场时就需要用保角变换。
电磁场的保角变换 在电磁场反演问题中,由已知远区场推算电磁场源的距离、方向和形状时,可采用保角变换,将已知二维闭合曲线的外域变换成单位圆的外域,并利用变换函数以及远区场两者的劳伦茨级数展开式的系数关系,可以得出解的低频估计。
在具体问题中,根据预给的势函数或流函数,去寻找合适的共轭函数并不容易。对于场域具有多角形边界的问题,施瓦茨变换是一种很有用的方法。它把一个复平面上由实轴和无限大的圆弧所围成的上半平面变换到另一复平面上的多角形内域,或反之。对于除了平角和零角之外只含一、二个正角的多角形,施瓦茨变换是初等解析函数;当正角增加到三、四个,变换与椭圆积分及椭圆函数有关。椭圆函数属于双周期解析函数,常应用于分析带状线等特种截面传输线。
核辐射与物质的相互作用,在原于和原子核物理、固体物理、核辐射探测和防护、核技术应用和核能利用等许多领域中有着重要的意义,对许多有关物理现象的分析、解释,以及在许多有关的实际商用、研究工作中实验方案和方法的确定,都要以射线与物质的相互作用为基础。
我们这里所说的射线(核辐射) ,泛指核衰变或核裂变放出的粒子和由加速器加速的离子或核反应产生的各种粒子,包括α,He,p、d,t 等重带电粒子,重离于和裂变碎片e、e等轻带电粒子,γ、X 射线,中子等。所说的物质,指各种化学元素,可以是单质,也可以是化合物或棍合物,可以是气体、液体和固体状态(包括无定形、多晶和单晶体) 。
下面将讨论α、β、γ射线、重离子和中子与物质的相互作用。由于α、β是带电粒子,而γ光子是不带电的,因此它们与靶物质原于发生作用的机制不同,它们的能量损失情况和粒于被物质吸收规律就不同,即使α、β及重离子都是带电粒子,由于它们的质量相差很大,它们在穿透靶物质时的行为也有不同,我们将分别加以讨论。中子与物质的相互作用,主要是中子通过核反应产生次级重带电粒子或中子诱发裂变的裂变碎片,这些二次粒子再与物质发生作用。至于其它高能粒子,它们与物质相互作用的行为有其特殊性,一般不包含在中低能核辐射与物质的相互作用的研究领域内。
-
带电粒子与靶物质原子的碰撞
α、β射线(或称粒子)和重离子穿过靶物质时,与靶物质原子的电于和原子核发生一系列相互作用。这些相互作用决定了带电粒子在靶物质中的命运,让我们来考察一下载能带电粒子穿透靶物质时的一般行为。
① 带电粒子在靶物质中的慢化
当一束准直的快速带电粒子(如α粒子) ,入射到靶物质(或称吸收物质和阻止物质)中,带电粒子与靶原子中的电子和与靶原子核发生库伦相互作用,主要是与靶原子中电子的碰撞。碰撞时发生动量和能量转移,入射粒子的一部分动能转移给靶原子中的电子或靶原子核。每一次碰撞时,靶原子中的电子获得的动能,相对于入射粒子的能量来讲,只是占其且能量的很小一部分,最大的为入射粒子能量E 的1/500,这里E 是每个核子的能量。例如,入射粒子为2MeV的α 粒子,每个核子能量为500keV.单次碰撞中,靶原子中一个电子获得的最大能量为lkeV。可见,这是一种小能量转移碰撞,每次碰撞后,入射粒子能量减少不多,方向几乎没有改变。所以入射带电粒子穿过靶物质时,要与靶原子中的电子连续地发生许多次这样的小能量转移碰撞,才逐渐损失能量。同时,随着粒子速度减慢,在速度小到一定程度时,要发生电荷交换效应。低速运动粒子从靶物质中俘获电子,从而使原来高速运动时完全剥离了电子的入射粒子,其有效核电荷数随粒子速度的减小而逐渐减少。如果靶物质厚度足够大,入射带电粒子与靶原子电子或靶原子核经过许多次碰撞后(例如,一个初始能量为1MeV 的重带电粒子,在靶物质中要经受10次弹性和非弹性碰撞) ,能使入射带电粒子能量全部耗尽,成为中性原子,停留在靶物质中,带电粒子阻止在靶物质中所需时间可以从它的射程和平均速度推算出来问。对MeV 量级的α 粒子和质子,整个慢化过程是在10s(气体物质中)到10 s(固体物质中)时间内完成的。
可见,载能带电粒子在靶物质中的慢化过程,完全是由带电位于与靶物质原子中的电子和与靶原子核发生各种相互作用的结果。归纳起来,带电粒子与靶物质原子的相互作用有下列四种
(1)与核外电子发生非弹性碰撞;
(2)与原子核发生弹性碰撞;
(3)与原子核发生非弹性碰撞;
(4)与核外电子发生弹性碰撞。
这些相互作用都是入射带电粒子在靶原子的核外电子和靶原子核的库仑场中的作用。当然,入射带电粒子也可以穿过原于核的库仑位垒,与原于核发生核反应,但它对带电粒子的慢化没有影响,带电粒子与物质的相互作用研究中一般不涉且带电粒子核反应过程。
下面我们再仔细看一下这四种碰撞过程所引起的入射带电粒子运动状革相靶物质原子状态的变化.
② 带电粒子与靶物质原子的碰撞过程
(1)带电粒子与靶物质原子中核外电子的非弹性碰撞
当带有正电荷或负电荷的载能粒子从靶物质原子近旁掠过时,入射粒子和靶原子的核外电子之间的库仑力作用,使电子受到吸引或排斥,从而使电子获得一部分能量。如果传递给电子的能量足以使电子克服原子的束缚,那么这电子就脱离原子,成为自由电子。这时靶原子就分离成个自由电子和一个失去了一个电子的原子——正离子,这种过程称为电离。原子最外层的电子受原子核的束缚最弱,故这些电子最容易被击出。电离过程中发射出来的自由电子,有的具有足够的动能,可继续与其它靶原子发生相互作用,进一步产生电离。这些高速的电子有时称为δ 射线。当原子的内壳层电子被电离后,在该壳层留下空位,外层电子就要向内层跃迁,同时放出特征X 射线或俄歇电子。
如果入射带电粒子传递给电子的能量较小,不足以使电子摆脱原子核的束缚成为自由电子,但可以使电子从低能级状态跃迁到高能级状态(使原子处于激发状态) ,这种过程称为激发。处于激发状态的原于是不稳定的,在激发态停留很短时间之后,原子要从激发状态跃迁回到基态,这种过程称为退激。退激时释放出来的能量以光的形式直射出来,这就是受激原子的发光现象。
带电粒子与靶原于中核外电子的非弹性碰撞,导致原子的电离或激发,是带电粒子穿过物质时损失动能的主要方式。我们把这种相互作用方式引起的能量损失称为电离损失,或者称它为电子碰撞能量损失或非弹性碰撞能量损失。从靶物质对入射粒于的阻止作用来讲,也可称电子阻止。
(2)带电粒子与靶原子核的非弹性碰撞
入射带电粒子靠近靶物质的原子核时,它与原子核之间的库仑力作用,使入射粒子受到吸引或排斥,结果使入射粒子的速度和方向发生改变。入射粒子的这种运动状态的改变,伴随着发射电磁辐射,并使入射粒子的能量有很大的减弱。当人射带电粒子与原子核发生非弹性碰撞时,以辐射光子损失其能量,我们称它为辐射损失。α粒子质量较大,与原子核碰撞后,运动状态改变不大。β粒子质量较小,与原子核碰撞后运动状态改变很显著,因此,β粒子与物质相互作用时,辐射损失是其重要的种能量损失方式。
带电粒子与靶原子核的非弹性碰撞,除了改变粒子的运动状志、辐射光子外,α粒子、质子和其它离子还可以使靶原子核从基态激发到激发态,这过程称为库仑激发,但发生这种作用方式的相对概率较小,可以起略不计。
(3)带电粒子与靶原子核的弹性碰撞
在弹性碰撞中,入射带电粒子靠近靶原子核时,由于它们之间的库仑相互作用,粒子同样受到偏转,改变其运动方向,但不辐射光子,也不激发原子核。在这弹性碰撞过程中,为满足入射粒子和原子核之间的能量且动量守恒要求,入射粒于损失部分动能,能量转移给原子核,使之反冲。碰撞后,绝大部分动能仍由入射粒子带走,但运动方向被偏转。这样入射带电粒子在物质中可继续与靶原子核进行许多次弹性碰撞。由这种靶原子核发生弹性碰撞引起入射粒子的能量损失,我们称它为弹性碰撞能量损失,或核碰撞能量损失。从靶物质对入射粒子的阻止作用来讲,也可称核阻止。带电粒子与靶原子核之间发生弹性碰撞时,原子核获得反冲能量,可以使晶格原子位移,形成缺陷,即造成靶物质辐射损伤。核阻止作用,只是在入射带电粒子能量很低时和低速重离子入射时,对能量损失的贡献才是重要的。同样由于β粒子比α粒子轻,β粒子所受到的偏转比α粒子严重,因此β射线穿透物质时,电子散射现象严重。
(4)带电粒子与靶原子中核外电子的弹性碰撞
入射带电拉兹也会与靶物质原子中的核外电子发生弹性碰撞。核外电子的库仓力作用,使入射粒子改变运动方向。当然,为满足能量和动量守恒要求,入射粒子要损失点功能,但这种能量转移一般是很小的,比原子中电子的最低激发能还要小,电子的能量状态没有变化.实际上,这是入射粒子与整个靶原子的相互作用。因此,这种相互作用方式只是在极低能量(100eV) 的β粒子入射到物质时方需考虑,其它情况下完生可以忽略掉。
以上讨论的入射带电粒子在靶物质中与靶原子的电子或原于核发生的各种相互作用方式其概率大小,对不同种类的带电粒子和粒子的不同能量区域,情况是十分不同的,而且,同种相互作用概率大小,与不同的靶物质元素也有关系。因此,这些相互作用中的各种作用方式对入射带电粒子的阻止作用的贡献大小不同,在一定的情况下,可只考虑某一种起主要贡献的相互作用,而忽略其它的相互作用。所以,在讨论载能带电粒子与物质相互作用的时候,常常要区分"轻"带电粒子(例如,电子和正电子)和"重"带电粒子(例如,质子、氘核和α 粒子等)。以及要区分快速和慢速粒于,分别进行讨论。比氦离子更重的重离子与物质的相互作用,将在重离于与物质相互作用中加以讨论。
-
重带电粒子与物质的相互作用
当载能重带电粒子入射到靶物质时,与靶原子发生相互作用而损失其能量。我们可以把这能量损失分成两部分与靶原子的核外电子的非弹性碰撞能量损失和与靶原子核的弹性碰撞能量损失,即电子阻止和核阻止两部分。对于快速的重带电粒子,主要是第一部分,而第二部分可忽略不计(后者比前者小三个量级)。只是在人射重带电粒子能量很低时,才需考虑核弹性碰撞对能量损失的贡献。由于重带电粒子的质量大,与电子非弹性碰撞后运动方向几乎保持不变,因此重带电粒子在物质中运动径迹近似是直线。由重带电粒子与靶原子核的非弹性碰撞引起的辐射能量损失,也完全可以理略掉。
① 重带电粒子在物质中的能量损失
(1)快速重带电粒子的能量损失
快速重带电粒子穿过靶物质原子电子云时,与电子发生非弹性碰撞,使入射粒子的一部分能量转移给电子,导致靶原子电离或激发。
根据量子理论并考虑了相对论和其它修正因子,推导出来的重带电粒子在靶物质中的电子阻止本领(电离能量损失率)精确表达式(称为Bethe-Block 公式)为:
式中β=v/c,c是真空中光速,方括号中的第二、三项是相对论修正值,I是靶原子的平均激发和电离能,它是能量损失率公式中的个重要参数,对每种靶元素的平均激发能的精确计算很难做到,通常认为它是一个由实验确定的经验参数。C/Z是壳修正项,是当入射粒子速度不能满足大于靶原于内层电子轨道速度这条件时,束缚得很紧的内层电子不能被电离和激发(即K ‘ L 、M 等内层电子不能参与对入射粒于的阻止作用)而引进的修正项。 这里的C=Ck 十CL十CM ... 。 壳修正项在入射粒子速度低时显得重要。
由上述的电于阻止本领理论公式,可以得到以下几点结论:
a.阻止本领只与入射粒子的速度有关(1/v),而与它的质量元关。这是由于重带电粒子质量比电子的静止质量大得多的缘故。
b.阻止本领与重带电位子的电荷数平方成正比。
c.阻止本领与靶物质的NZ 有关。高原子序数和高密度物质具有较大的阻止本领.
(2)低速重带电粒子的能量损失
当重带电柿子的速度低于轨道电子的平均速度归 在前面讨论高速和低速重带电粒于的能量损失时,只是考虑了与靶原于的电子碰撞引起的电离损失(电子阻止)。认为入射粒子与靶物质原子核的弹性碰撞引起的能量损失(核阻止)相对于入射粒子与电子的非弹性碰撞引起的能量损失来讲是不重要的。对p 和α粒子,只是在很低能量时,才需考虑核阻止的贡献,这时核阻止作用的贡献可以与电子阻止作用的贡献相比较,甚至能超过电于阻止作用的贡献。当入射离子是低速重离子时,核阻止作用就显得重要了,这将在重离于能量损失时进步讨论。 如果我们把从低能到高能的重带电粒子的阻止本领与入射粒子能量E 的关系,画成下图所示的曲线(图中横坐标以靶物质的静止能量为单位)。我们看到在高速Bethe-Block 公式适用区域,(dE/dx)e正比于(1/v),速度稍低时,应考虑壳修正。在低速区,(dE/dx)e正比于v,这是低速区的最为显著的特点。在中理区尚无告适的理论计算公式,实际使用时都是一些实验数据的拟古公式。 (4)能量歧离现象 在前面讨论重带电粒子能量损失时,我们已知道带电粒子是与靶物质原子中的电子和靶原子核发生许多次碰撞而损失能量的。对任何个特定的入射粒子来说,它沿着径迹所经历的碰撞拉数及每次碰撞时所转移的能量都是随机变化的。对一柬具有相同能量的入射粒子来讲,它们在靶物质中碰撞过程的统计涨落,使能量损失有一分布(也就是相同能量的入射粒子,在靶物质中穿过同距离后,这些粒子的能量损失不是相等的)。我们前面所说的能量损失是对所有入射粒子求平均而得到的平均能量损失,而每个别粒子的能量损失是在这平均值附近涨落。这种能量损失的统计分布称为能量歧离。能量损失的歧离卦布可以用高斯分布来描写。 例如,3MeV 的单能质子束,穿过3.3mg/cm2的金箔后,能量减小了0.117MeV,而能量分散性增加5 倍(穿透前谱线的半宽度FWHM 是6. 5keV ,穿过物质后是34. 4keV),如下图所示。 所以,当一柬单能重带电粒子入射到靶物质上,在表面时,能量分布很窜,越到靶子深部,平均能量越来越小,能量分布越来越宽。在进行核物理实验测量时,特别是能谱分析时,应考虑这种谱线展宽现象。 ① 重带电粒子在物质中的射程 (1)比电离 重带电粒子穿过靶物质(也称吸收体)时,使物质原于电离,产生电于离于对。这是人射粒子直接引起的电寓,称为原电离。电离过程中班出的δ电子,具有几千电子伏的动能,它可以进一步引起原子电离,产生更多的电子离子对,称为次电离。在吸收体中总的电离是这两部分电离之和,已知重带电粒于在物质中单位路程上的能量损失是与粒子速度、粒子的电荷态有关的,所以单位路程上产生的电子离子对数目也就与粒子速度和电荷态有关。同种粒子,速度慢的在单位路程上产生的电子离子对数目较多;速度相同的粒子,电荷态高的,在单位路程上产生的离子对数目较多。因此,重带电粒子贯穿物质时,从路程的开始端到路程的末端(粒子速度等于零),路上所产生的电子-离子时数目分布是不均匀的。我们把单位路程上的离子对数目称为比电离,以S表示,下图是α粒子和质子的比电离测量结果。当粒子接近它的路程末端时,比电离达到最大值,这对应于电离损失率的最大值。越过峰值之后,由于粒子能量几乎耗尽,比电离骤然下降,很快就降到零。.比较图中给出的α粒子和质子的比电离曲线。 (2)α粒子的射程 带电粒子在物质中运动时,不断损失能量,待能量耗尽,就停留在物质中。它沿原来入射方向所穿过的最大距离,称为入射粒子在该物质中的射程,以R表示。应当指出,“射程”和“路程”是两个平同的概念,射程(投影射程)是指入射粒子在吸收物质中,沿入射方向从入射点到它的终止点(速度等于零)之间的直线距离,亦即沿入射方向穿透的深度。而路程则是入射粒子在吸收体中所经过的实际轨迹的长度。一般路程大于射程,路程在入射方向上的投影就是射程。 重带电粒子的质量大,它与核外电子非弹性碰撞和它与原于核的弹性碰撞作用,不会导致入射粒子的运动方向有很大的改变,它的轨迹几乎是直线,因此可以认为射程近似地等于路程长度。 上图画出了测量α 粒子在空气中的射程的实验装置,一端放置一个α放射源,α射线经准直器准直后进入α粒子探测器进行计数,探测器可沿α粒子的出射方向移动。改变探测器离源的距离,测量α粒子的计数率,即可得到图(b)中所示的曲线a。在开始一段距离时,计数率保持不变,表明α粒子没有被空气吸收。当增加到一定距离时,计数率很快下降, 直降到零。这显示α粒子贯穿了这距离的空气层被吸收掉,全部停留在附近的区域内。距离为时,α粒子的计数降至原来的一半。对曲线a 求导,便可得到曲线b。曲线b 代表单位路程上的α粒子数的变化按路程的分布,称为微分曲线。它表示大多数α粒子停留在处,就是α位于在空气中的平均射程。由于碰撞过程的统计涨落,不仅引起能量歧离,而且还造成粒子在物质中的射程歧离现象,即能量相同的人射粒子束,它的射程长短有一分布,个别粒子的射程是在平均值附近涨落的。p,a等重带电粒子,射程涨落的大小是平均射程值的百分之几。相同速度的p 和α粒子,在同一物质的射程相同,但质子的射程歧离是α粒子的射程歧离的两倍。对低速的离子,电子阻止对射程歧离的贡献可忽略,主要是核阻止过程决定着射程歧离。另外,一束具有相同人射方向的带电粒子,与靶核碰撞而产生小角度偏转。在靶物质中穿过一定厚度时,许多次碰撞结果,导致粒子角度偏转有分布。多数沿着入射束方向出射,部分粒子偏离原来方向,向两侧出射,即存在着角度(运动方向)歧离,可用角度偏转的均方值来表示。我们测量或计算的射程都是指平均射程而言.射程的单位可用cm 或mg/cm 表示。α粒子、质子在不同物质中的射程与能量关系有图表可查,也有计算机程序可计算,其中TRIM 程序己广泛应用。
重离子与物质的相互作用
由于重离子核反应方面的研究工作和半导体材料、金属材料中离子注入研究且重离子柬表面层分析工作等迅速开屉,迫切需要了解重离于与靶物质相互作用的行为和重离子在物质中的阻止本领数据。
所谓“重离子”,是指z>2 的所有失去了部分电于的原于(正离子),或有过剩电子的原子(负离子),一般都是指正离子。有时把裂变碎片也归并在这儿起讨论,找们前面讲重带电位子与靶物质原子相互作用。当一定电荷态的重离于穿过靶物质时,除了上述的入射离子的原于核与靶原子电子和靶原子核之间的作用外,还有靶原子核与入射离子中束缚电子之间的库仓作用,以及入射离子中的电子与靶原子中电子之间的相互作用。离子的束缚电子与靶原子电子之间的相互作用,对阻止本领的贡献是很小的,只是在重离于速度很低时,才予考虑。当离子速度大时,主要是通过电离(包括多重电离)、激发靶原子过程使离子慢化。所以重离子在物质中的能量损失机制,与质子、α粒子等重带电粒子的能量损失机制相比较,原则上讲没有本质的不同。如果离于能量很高,离子的核外电子完全被剥离时,前面讲的能量损失率公式式也是适用的。但由于重离子的内层电子束缚得很紧,一般不能使重离于的轨道电子全部剥离,离子的电荷态并不等于它的核电荷数。而且,当重离子穿过靶物质时,离子的电荷在要发生变化。这与前面讨论的快速运动的p 和α粒子时的情况不同。在讨论快速质子和α粒子的能量损失时,通常认为可以组略的一些因素(主要有两方面因素:①电荷交换效应,②核阻止作用),却起着重要的作用。
-
β射线与物质的相互作用
这一节里我们讨论轻带电粒子(包括β射线、单能电子以及正电子)与靶物质的相互作用。电于质量小,所以它在物质中的能量损失情况和运动轨迹与重带电粒子相比很不一样。电子与靶原子的作用,主要引起电离能量损失、辐射能量损失和多次散射。电子在物质中的运动径班则十分曲折。
(1)电子的能量损失
a. 电离损失
快电子通过靶物质时,与原子的核外电子发生非弹性碰撞,使物质原子电离或激发,因而损失能量,这与重带电粒于情况相类似。电离损失(电子碰撞能量损失)是β射线在物质中损失能量的重要方式。但由于入射电子质量与跟它发生相互作用的靶原子轨道电子质量一样,一次碰撞损失很大部分能量(最大能量转移可为电子能量的一半,大多数情况下的平均能量转事为几个keV)。 碰撞后入射电子运动方向有较大的改变。由非弹性碰撞所引起的电子能量损失的表达式,在低能时为:
在高能时,应考虑相对论效应,表达式为:
式中E 为人射电子的动能(总能量一静止能量)。我们可以看到,上式与重带电粒子的Bethe-Block 公式相比,电子的(-dE/dx)也是与粒子的速度平方成反比。在能量相同的情况下,电子的速度比α粒子的速度大得多,因而电子的电离损失率比α粒子要小得多。而它穿透物质的本领比α粒子大得多。
由于β粒子的能量损失率较小,所以β粒子的比电离值较小,即β粒子的电离本领是较弱的。相协日, 4MeV的α粒子,在水中每微米能产生3000 对电子-离子对,而1MeV 的β粒子每微米只产生5 对。
b. 辐射损失
β粒子穿过物质时,除了使原子电离或激发损失能量外,还有另一种损失能量的方式——辐射损失。这是β粒子与物质原子的原子核非弹性碰撞时产生的一种能量损失。根据经典电磁理论,当带电粒子接近原于核时,速度迅速减低,会发射出电磁波(光子)。这种电磁辐射叫轫致辐射。例如,入射带电粒子受到靶物质原子核库仑场的作用,使它的运动速度大小和方向发生变化,即有加速度时,总是伴随着发射电磁波。如X光管中,电子束打到钨靶上就产生韧致辐射(X 射线)。电子加速器的高能电子束轰击靶子产生韧致辐射。
根据电磁理论,电磁波的振幅正比于加速度,而加速度正比于入射带电粒子和原子核之间的库仑力,即加速度正比于zZ /m 。因此,电磁辐射的强度(对各种能量的光子积分)正比于振幅的平方。根据量子电动力学可以得出,韧致辐射引起的电子辐射能量损失有如下的关系:
式中m 是入射粒子的质量;E为入射粒子能量;z和Z分别为人射粒子的电荷数和靶物质的原子序数;N为单位体积中物质的原子数;脚标r表示辐射损失;c 为光速。从式中可以看到:
辐射能量损失率与z成正比,与m成反比。因此,电子的辐射损失率,或电子的韧致辐射强度比α粒于、质子和重离子要大得多,因此,对重带电粒子和重离子的韧致辐射引起的能量损失完全可以理略不计。
辐射能量损失率与Z成正比。表明电子打到重元素靶物质中,容易发生韧致辐射.这一特性对选择合适的材料来阻挡β粒子很重要。因为电离损失率与Z 成正比,从电离损失考虑,采用用高Z元素来阻挡β粒子; 然而,这生产生很强的韧致辐射,反而起不到防护作用,所以应采用低Z元素防护β粒子。
辐射能量损失率与粒子能量E成正比。这点与电离损失是不同的,所以电于能量低时,电离损失占优势;能量高时,辐射损失变得重要了。电子的总的阻止木领为碰撞损失(电离损失)和辐射损失之和。
对于铅Z=82,当E>10MeV 时,两种能量损失的相对重要性明显变化。而时于水和空气,当E>100MeV 时,两种损失的贡献大小明显不同。对于常用的β放射源,电子能量不过几个兆电于伏,因此主要的仍是电离损失。由电子加速器引出的电子束,能量较高,而且束流较大,因此韧致辐射强度根强。
在韧致辐射过程中,入射电子原来的动量由原子核、光子和被偏转的电子三者之间分配,所以韧致辐射光于可以具有任何动量值,对应的光子能量, 是连结谱。能量从零到最大值等于电子的动能,故韧致辐射也称连续X射线。能量低时,光子带走的动量较小,所以光子向各个方向发射;能量高时,光于倾向于前向发射。下图给出了电子在铍和金中的韧致辐射强度(对所有能量的光子积分)的角分布。
带电粒子穿过物质时发射电磁辐射的现象,除了韧致辐射外,还有另一种辐射过程——切伦科夫辐射。这是带电粒子使原子暂时极化,当退极化时,发射光子。
(2)电子的散射
β粒子与靶物质原子核库仑场作用时,只改变运动方向,而不辐射能量,这种过程称为弹性散射。由于电于的质量小,因而散射角度可以很大(与α 粒子相比,β粒子的散射要大得多),而且会发生多次散射,最后偏离原来的运动万向。同时,入射电子能量越低,且靶物质的原子序数越大,散射也就越厉害。粒子在物质中经过多次散射,其最后的散射角可以大于90" ,这种散射称为反散射。低能电子在高原子序数Z厚样品物质上的反散射系数高达50,所以在实验中,宜用低Z物质来做源的托架,以减少反散射对测量结果的影响。然而J 粒子的
(3)β射线的射程和吸收
β粒子和重带电粒子在物质中的射程有着显著的差异。首先β粒子的能量损失率比α 粒子小,因此它比α粒子具有更大的射程。例如,在空气中,能量为4MeV 的β射线,射程是15m;而相同能量的α粒子,射程只有2.5cm。此外,α粒子与靶原子电子多次碰撞逐渐损失能量,几乎是直线行走的,只是在射程末端与靶原子核的碰撞才使径迹有些偏离直线,因而α粒子有确定的射程(平均射程)概念。α粒子的射程与径迹长度近似相等,粒子数只是在平均射程附近有明显的吸收。只是由于能量歧离效应,存在射程歧离现象。而对电子来讲,射程概念不如重带电粒子时那样确切。由于电子质量小,在电离损失、辐射损失和与核的弹性散射过程中,电于运动方向有很大的改变,这样使β粒于穿过物质时走过的路程十分曲折。因而路程轨迹长度远大于它的射程。一束准直的单能电子入射到靶物质中后,由于能量损失的统计涨落较大和多次散射现象,电子的射程的不确定性大大增加。射程歧离可达射程值的10%-15% 。歧离效应较大是因为在如射电子与靶原子电子的非弹性碰撞和在辐射能量损失中,能量转移总是较大所致。
β射线或单能电子束穿过一定厚度的吸收物质时,强度减弱的现象叫吸收.下图是观察β射线吸收现象的实验装置示意图。让β射线穿过吸收片后,到达探测器。记录它的强度随吸收片厚度的变化,作图得到吸收曲线。
先讨论单能电子束。由于电于的散射厉害,即使吸收片很薄时,有部分电于也会偏离原来的入射方向,不能到达探测器;只有方向改变小的那些电子才能到这探测器被记录。所以单能电子的吸收曲线(b)一开始就立即下降。图中纵坐标为透射率,以线性坐标表示。当吸收片厚度增加时,电子能量不断损失,散射偏转越来越大,到达探测器的电子数越来越少,渐渐趋近于零。单能电子的吸收,粗略地是随厚度线性变化的。它与单能α粒子的吸收曲线很不一样。 一般把单能电子的吸收曲线的线性部分外推到零,来定出电子的射程——外推射程。电子束的平均射程近似等于平均路程的一半。电子通过物质时,不仅能量减小,而且能量歧离现靠很严重。
对于β粒子,能量连续分布,它的吸收曲线与单能电子的吸收曲线有明显的不同。即使吸收片很薄时,β谱中能量低的电子很快被吸收,因此,β吸收曲线的开始部分斜率变化更大。对β谱中每小能量间隔内的电子,可以认为它遵循线性吸收规律,但由于β谱中电子能量连续分布,和不同能量的电子其吸收曲线的斜率不同,线性迭加结果,对β谱的主要部分来讲,吸收曲线近似地为指数曲线,如图(c)所示.因此,对β粒子没有确定的电子射程可言。可以用与β射线能谱中电于最大能量所对应的射程来表示β射线的射程,称β射线的最大射程Rmax,在吸收曲线上外推到净计数为零的地方,与横轴主点即为最大射程。
另外,与在讨论重带电粒子的能量损失与射程时一样,在讨论电子的能损和射程时用质量厚度来表示靶厚度是很有用的。粒子穿过相同质量厚度的不同吸收物质时,与粒子发生碰撞的电子数目大体相同,所以用质量厚度表示时,对Z相差不是太大的靶物质,其阻止本领和射程大体是相同的, dE/ρdx正比于Z/A,对绝大多数元章,Z/A=I/2,对那些原子序数相近的物质(例如空气、铝、塑料和石墨等),尽管它们的密度差异很大,射程值(以质量厚度为单位)却近似相同。
(4)正电子与物质的相互作用
正电子通过物质时,也和负电子样,要与核外电子相原子核相互作用,产生电离损失、辐射损失和弹性散射。尽管负电子和正电子与它们作用时受的库仑力或为排斥力或为吸引力,因它们的质量相等,因此能量相等的正电子和负电子,它们在物质中的能量损失和射程是大体相同的。上述对于负电子的讨论,对于正电子也同样适用。可是,正电于有其明显的特点。 高速正电子进入物质后很快被慢化,然后在正电子径迹末端遇负电子即发生湮没,放出γ光子;或者,与一个负电子结合在一起,形成正电子素,衰变后转变成电磁辐射(即形成正电子素后才湮没。正负电子湮没放出的γ光子称为湮没光于。从能量守恒考虑,在发生湮没时,正、负电子动能为零,所以两个湮没光子的总能量应等于正、负电子的静止质量。同时,从动量守恒考虑,由于湮没前的正、负电子的总动量等于零,湮没后,两个湮没光子的总动量也应为零。因而,两个湮没光子能量相同,各等于m0C=0. 511MeV。两个光子的发射方向相差近似180度。并且湮没光子的发射是各向同性的。0. 51l MeV 的光子贯穿靶物质的深度比正电子射程大,导致能量沉积远超过原来的正电子径迹范围。
(5)γ射线与物质的相互作用
(1)γ射线与物质相互作用的一般特性
γ射线、韧致辐射、湮没辐射和特征X射线等,虽然它们的起源不一、能量大小不等,但都属电磁辐射。电磁辐射与物质相互作用的机制,与这些电磁辐射的起源是无关的,只与它们的能量有关,所以我们这里讨论的γ射线与物质的相互作用规律,对其它来探产生的电磁辐射也是适用的。
γ射线与物质的相互作用和带电粒子与物质的相互作用有着显著的不同。γ光子不带电,它不像带电位于那样直接与靶物质原子、电子发生库仑碰撞而使之电离或激发,或者与靶原子核发生碰撞导致弹性碰撞能量损失或辐射损失,因而不能像带电粒子那样用阻止本领dE/dx和射程来描写光子在物质中的行为。带电粒子主要是通过连续地与物质原子的核外电子的许多次非弹性碰撞逐渐损失能量的,每次碰撞中所转事的能量是很小的(小能量转移碰撞)。而γ光子与物质原子相互作用时,发生一次相互作用就导致损失其大部或全部能量(大能量转移),光于不是完全消失就是大角度散射。
γ射线与物质相互作用,可以有许多种方式。当γ射线的能量在30MeV 以下时,在所有相互作用方式中,最主要的三种是:
-
光电效应。γ光子与靶物质原于相互作用,光子的全部能量转移给原于中的束缚电子,使这些电子从原于中发射出来。γ光子本身消失。
-
康普顿效应(又称康普顿散射)。入射γ光子与原子的核外电子发生非弹性碰撞,光子的一部分能量转移给电子,使它反冲出来,而光子的运动方向和能量都芷生了变化,成为散射光子。
-
电子对效应。γ光子与靶物质原子的原子核库仑场作用,光子转化为正负电子对。
除了上述三种主要相互作用方式外,其它一些相互作用方式有:
相干散射。低能光子(hν<
光致核反应。大于一定能量的γ光子与物质原子的原子核作用,能发射出粒子,但这种相互作用的大小与其它效应相比是很小的,所以可以忽略不计。
核共振反应。入射光子把原子核激发到激发态,然后退激时再放出γ光子。
光子能量在100keV ~ 30MeV 范围内,所有这些次要的相互作用方式对于γ射线的吸收所作的贡献小于1 %,所以下面我们只讨论前面三种主要作用方式。
γ射线与物质发生上述三种主要相互作用都具有一定的概率。我们用截面σ这个物理量来表示作用概率的大小。因此有各种作用截面光电效应截面、康曹顿散射截面和电子对效应截面,这些截面称为部分截面,γ射线与物质相互作用的总截面是这些部分截面之和。
截面大小与γ射线能量和靶物质性质有关。下面我们分别讨论这三种主要相互作用方式。
(2)光电效应
γ光子与靶物质原子的束缚电子作用时,光子把全部能量转移给某个束缚电子,使之发射出去,而且本身消失掉,这种过程称光电效应。光电效应中发射出来的电子叫光电子。这过程如下图所示。
原子吸收了光子的全部能量,其中一部分消耗于光电子脱离原子束缚所需的电离能(电子在原于中的结合能)。另一部分就作为光电子的动能。所以,释放出来的光电子的能量就是入射光子能量和该束缚电子所处的电子壳层的结合能之差。虽然有一部分能量被原子的反冲核所吸收,但这部分反冲能量与γ射线能量相比可以起略。因此,要发生光电效应,γ光子能量必须大于电子的结合能。光电子可以从原子的各个电子壳层中发射出来,但是自由电于(非束缚电子)却不能吸收入射光自能量而成为光电子。这是因为动量守恒要求,在光电效应过程中,除入射光子和光电子外,还需要有个第三者参加,这第三者就是原子核,严格地讲是发射光电于之后剩余下来的整个原子。它带走些反冲能量,但这能量十分小。由于它的参加,动量和能量守恒都能满足。而且,电子在原子中束缚得越紧,就容易使原于核参加上述过程,产生光电效应的概率也就越大。所以在K 壳层上打出光电子的概率最大,L 层次之, M、N 层更次之。如果入射光子的能量超过K 层电子结合能,那么,大约80%的光电吸收发生在这K 层电子上。
发生光电子效应时,从原子内壳层上打出电子,在此壳层上就留下空位,并使原子处于激发状态。这种激发状态是不稳定的,退激的过程有两种,一种过程是外层电子向内层跃迁,来填补这个空位,使原子恢复到较低的能量状态,两个壳层的结合能之差,就是跃迁时释放出来的能量,这能量将以特征X射线形式释放出来。另一种过程是原子的激发能交给外壳层的其它电子,使它从原子中发射出束,这电子称俄歇电子。因此,在发射光电子的同时,还伴随着原子发射的特征X射线或俄歇电子。这些特征X射线和俄歇电子再与靶物质原子发生作用。
光电子的能量
在光电效应中,可以由能量守恒定律得到。
光电截面
我们把光电效应截面简称为光电截面。光电截面太小与γ射线能量和吸收物质的原子序数有关。关于光电截面公式,可由量于力学计算得到。在非相对论情况下,K层的光电截面为:
在相对论情况下,K层的光电截面为:
所以在两种情况下,都有 σ k 正比于Z的关系,随Z的增大,光电截面迅速增大。这是因为光电效应是γ光子和束缚电子的作用,Z越大,则电子在原于中束缚得越紧,越容易使原子核发生光电过程来满足能量和动量守恒要求,因而产生光电效应的概率就越大。由于这一事实,我们往往果用高原子序数的材料来探测γ射线,以获得较高的探测效率。由于同样的原因,也选用高Z物质作为γ射线的屏蔽材料。
从上两式还可以看到, σ k随 hν增加而减小。低能时,变化得更快一些,高能时,变化缓慢一些。这一变化趋势,可粗略地这样来说明。γ射线能量低时,相对而言,电子被束缚得也就越紧,越容易发生光电效应;而当γ射线能量高时,电子的束缚能相对来说可以忽略不计,这种电于接近“自由电子”,所以光电效应截面就小。
下图给出了不同吸收物质的光电截面与光子能量的关系,也称光电吸收曲线。从图中可以看出,随E的增大, σ ph变小,而随Z的增大, σ ph增大。
在 hν<100keV 时,光电截面显示出特征性的锯齿状结构,这种尖锐的突变,称为吸收限。它是在入射光子能量与K、L、M层电于的结合能相一致时出现的。当光子能量逐渐增加到等于某一层电子的结合能时,这一壳层的电子就对光电作用有贡献,因而 σ ph就阶跃式地上升到某一较高的数值,然后 σ ph随能量的增加而下降。图(b)是铅的光电吸收曲线, K 吸收限为88.3keV 。对L、M层电子,存在着子壳层,各子壳层的结合能稍有差异,因而吸收曲线中对应于L吸收限和M吸收限存在着精细结构。L层有3 个吸收限,M层有5个吸收限。这种吸收限特性可用来选择性地降低某种γ辐射强度或者用来转换(激发)某种特征X 射线。
光电子的角分布
相对于γ光子的入射方向而言,在不同的角度光电子的产额是不一样的。首先我们从光电过程中能量和动量守恒来看,要是这过程中没有第三者(原于核)参加,光电子就应从γ光子入射方向(定为0度方向)飞出。而实验上在0度方向没有观察到光电子,这就证明光电过程中有第三者参加,光电子就不能从0 度方向发射。实验和理论计算都证明,在180度方向也不能出现光电子,而在某一角度,光电子出现的概率最大。在入射γ光子能量很低时,光电于在垂直于入射γ束方向上发射,当γ能量增加时,逐渐朝前方角发射.下图表示同γ能量下,光电子发射的角分布。
(3)康普顿效应
康普顿效应是人射γ光于与原子的核外电子之间宜生的非弹性碰撞过程.这一作用过程中,入射光子的一部分能量转移给电子,使它脱离原子成为反冲电子,而光子的运动方向和能量发生变化,如下图所示。 hν和 hν’ 为入射和散射光子的能量;θ为散射光子与入射光子方向间的夹角,称散射角;φ.为反冲电子的反冲角。
康普顿效应与光电效应不同。光电效应中光子本身消失,能量完全转移给电子;康曹顿效应中光子只是损失掉部分能量。光电效应发生在束缚得最紧的内层电子,康普顿效应总是发生在束缚得最松的外层电子上。虽然光子与束缚电子之间的康普顿散射,严格地讲入射光子是一种非弹性碰撞过程。但外层电子的结合能是较小的,一般是电子伏数量级,与入射γ光子的能量相比较,完全可以忽略,所以可以把外层电子看作是“自由电子”。这样康普顿效应就可以认为是γ光子与处于静止状态的自由电子之间的弹性碰撞。人射光子的能量和动量就由反冲电子和散射光于两者之间进行分配。用相对论的能量和动量守恒定律,可以推导出这种碰撞中散射光自和反冲电子的能量与散射角的关系。
散射光子和反冲电子的能量与散射角的关系
当散射角为0度时,散射光子能量达到最大值,这时反冲电子的能量等于0。 这就是说,在这种情况下,入射光于从电于近旁掠过,未受到散射,所以光子能量没有损失。当散射角为180度时,入射光子与电子对心碰撞后,沿相反方向散射回来,而反冲电子则沿入射光子方向飞出,这种情况称反散射。这时散射光子能量为最小值,而反冲电子的功能达最大值。
下图给出了单个电子的微分散射截面与散射角、能量的关系。入射光子能量越高,散射光子越是朝前向散射。
反冲电子的能谱和角分布
发生康晋顿效应时,散射光子可以向各个方向散射。对于不同方向的散射光于,其对应的反冲电子能量也不同。因而即使入射γ光子的能量是单一的,反冲电子的能量却是随散射角连续变化的。由于散射光于和反冲电子的方向有一一对应关系,在θ角度发射散射光子,相应于在 Φ角度发射反冲电子。散射光子数和反冲电子数是相等的。
下图给反冲电子截面与反冲角的关系。从图中可以再次看到,反冲电子只能在小90度方向发射。
任何一种单能的γ射线所产生的反冲电子的功能都是连续分布的。在反冲电子的最大能量处,反冲电子数目最多,而在较低能量处,电子数大体相同。
(4)电子对效应
当γ光子从原子核旁经过时,在原子核的库仑场作用下,γ光子转化为一个正电子和一个负电子,这种过程称为电子对效应。如下图所示。
与光电效应相似,电子对效应除涉及入射光子和电子对以外,必须有一个第三者——原子核参加,才能满足能量和动量守恒定律。过剩的动量必须被参与这过程的第三者原子核带走,因原子核质量大,反冲能量很小,可以忽略不计,故上式成立。
对于一定能量的入射光子,电子对效应产生的正电子和负电子的功能之和为常数。但就电于或正电子某一种粒子而言,电子和正电子之间的能量分配是任意的。由于动量守恒关罩,电子和正电子几乎都是沿着入射光子方向的前向角度发射的。入射光于能量越大,正负电于的发射方向越是前倾。
电子对过程中产生的快速正电于和电子,在吸收物质中通过电离损失和辐射损失消耗能量。正电子在吸收体中很快被慢化后,将发生湮没,湮没光子在物质中再发生相互作用。
正、负电子的湮没,可以看作是γ射线产生电子对效应的逆过程。电子对效应,要用狄拉克的电子理论来解释。
核辐射探测常见核辐射探测器
核辐射探测器的物理基础是核辐射和物质的相互作用,利用核辐射在气体、液体、固体中的电离效应、发光现象、物理或化学变化进行核辐射探测与测量的元件称为核辐射探测器。
核辐射探测器从核辐射开始被发现时起,使用了气体电离室、照相底片和晶体探测器,到现在已有一百多年的历史。随着科学技术的发展、核物理实验和核科学研究的深入、核技术应用领域的扩大,核辐射探测器和探测系统也发生着显著的变化。目前常用的核辐射探测器有:气体探测器、闪烁体探测器和半导体探测器,它们是随着科学技术的发展和核物理、粒子物理实验和其它应用的需要,在不同的时期开发研制并逐渐完善成目前所具有的探测器系列。它们之间由于各自有各自的优缺点,所以在某一或某些应用中起着主导作用,但它们之间并不存在谁能完全代替谁而将其淘汰,而是随着科学技术的发展,相互共存并都在不断的创新发展,促使核辐射探测器及探测系统跟着发生显著的变化。
核辐射探测气体探测器
气体探测器是在19世纪末20世纪初核辐射能被发现时最早被使用的一种探测器,当时使用的是空气电离室,它在早期的核物理和核科学研究中起到了重要的作用。到20世纪60年代末就已研制、生产了一系列的气体核辐射探测器。如G-M(盖革-米勒)计数管,根据淬灭气体的不同又分为有机G-M管和卤素G-M管,还有流气式大面积G-M计数管、端窗管;电离室有:脉冲电离室、屏栅电离室、衬硼电离室、电流电离室、裂变电离室、补偿电离室、自由空气电离室、空气等效电离室;正比计数管有:BF3(三氟化硼)正比计数管、位置灵敏正比计数管、3He正比计数管、多丝正比管,还有漂移室、平行板雪崩室。
虽然气体探测器在某些应用领域内(如带电粒子能量(能谱)测量)已基本上被半导体探测所取代,但由于它具有结构简单、使用方便、可制作成各种较大型的电离室,因此在工业领域仍得到了广泛的应用,如料位计、核子秤、厚度计、中子水分计等。
到20世纪80年代末,Xe气体纯化技术的提高,促进了Xe闪烁正比计数管的发展,构成了新型的Χ射线Xe气体闪烁正比计数管。与一般的正比计数管相比,GSPC(气体闪烁正比计数管)能量分辨率高。例如:对55Fe 5.9keV X射线,Xe GSPC的FWHM为472eV;对0.15keV的X射线,FWHM为85eV,噪声仅为50eV,可鉴别硼的Kx射线,比一般正比计数管的能量分辨提高了一倍。Xe气体的法诺因子为0.17±0.007,电荷倍增没有产生空间电荷,所以计数率可高达90kcps,并可构成面积为200cm2的大面积探测器。这种探测器也可用于人造卫星上来测量宇宙X射线,并可用于穆斯堡尔实验、荧光X射线谱的测量、环境放射性的监测等。另外,球形电离室、重离子电离室等新产品的相继研制成功,越来越受到了人们的重视。高压Xe电离室线性阵列探测器,探测器的一致性较好,并可做到很高的排列密度,是近10年来在我国首先应用于集装箱安检成像系统的核辐射线性阵列探测器。缺点是气体对射线的吸收(衰减)效率低,探测效率小于60%,所以一般用于能量较低的场合。
核辐射探测闪烁体探测器
闪烁体探测器是指由闪烁体与光敏元件(包括光导、光学耦合剂、集光系统)一起组合成的探测元件称为闪烁体探测器。它早在20世纪40年代问世,20世纪50年代初,(NaI/Tl)闪烁计数器商品化,使γ射线能谱测量成为一般实验室内均能做到的常规实验。随着核物理、粒子物理实验、核科学研究的发展,促进了对闪烁体的研制开发,构成了多种类型闪烁体:如无机闪烁体NaI(Tl)、CsI(Tl)、BaF2、ZnS(Ag)、LiI(Eu)等;有机闪烁体(多属于苯环结构的芳香族碳氢化合物),如蒽晶体、菧晶体、萘晶体、塑料闪烁体、玻璃闪烁体等。到20世纪70年代中期,又开发出适合高能γ射线探测的、可以适用于任何空间有限、而且要对γ阻止本领大的场合的BGO(锗酸铋Bi4Ge3O12)无机闪烁体,它是一种纯的本征晶体,化学稳定性好、不潮解、机械强度好,闪烁体衰减时间短、余辉小,特别适用于Χ射线断层照相、工业密度计和测井用,因而获得了愈来愈多的应用。另一种是可以配用硅光电二极管(作为光敏器件)的钨酸镉(CdWO4)闪烁晶体,它兼有对γ射线的阻止本领高和较理想的闪烁性能两种优点,对阻止150keV的γ射线,衰减90%的厚度仅需3mm厚,非常适合于对空间分辨率要求高的场合,如核辐射成像阵列探测器。
由于NaI(Tl)极易潮解,所以它必须密封封装;CsI(Tl)虽在空气中也会潮解,但只是局部表面受损,将表面重新加工处理后一般可使原来的性能恢复。另外它的闪烁光谱性能与硅光电二极管的光谱性能较匹配,所以CsI(Tl)闪烁体最好与硅光电二极管光敏器件组合。闪烁探测器在测量能量低于5MeV的γ射线能谱时,常出现散射光子或湮灭光子逃逸闪烁体的事件,导致低于光电峰的连续谱的形成,这是工作中不希望的。当γ射线能量增高时,这类逃逸事件产生的机率增大,使对高能谱线的分析变得困难。所以在工作中是选用NaI(Tl)还是CsI(Tl)要根据要求来选择。对同样大小的晶体,要得到大的峰总比,则选用CsI(Tl);要得到给定的某一能量的峰总比,则选用尺寸较小的CsI(Tl)晶体。
为配合高能物理和Χ、γ射线成像方面的应用,在原来的NaI(Tl)、CsI(Tl)、BGO、CdWO4基础上又研制了LuAP铝酸镥(LuAlO3)、LSO硅酸镥(Lu2SiO3)、SGD硅酸钆(Gd2SiO4)、GOS硫氧化钆(Gd2O2S)和YAP铝酸钇(YAlO3)。
为了提高闪烁体探测器对低能γ射线测量的能量线性度,在闪烁体探测器测量γ射线能量时因为闪烁光的产额随能量变化,所以用闪烁体探测器测量低能γ射线时存在着能量的非线性。241Am和57Co这两种低能γ射线放射源的γ射线能量的比值为0.488,任何实测能谱中对应于这两种γ射线光电峰的峰位比值的偏离都是非线性的表现。为扩展闪烁体在X光安检成像方面的应用,在近一两年内已研发出一种新型的闪烁体——氯化镧[LaCl3(Ce)],它具有引人注目的闪烁性能,LaCl3掺 3Ce作为激活剂,具有非常高的光输出49000光子/MeV,而且主成分发光衰减的时间很快(26ns),这些性质使得LaCl3(Ce)成为一种很有希望的探测γ射线的材料。另外,对于低能γ射线的能量测量时,在低能端LaCl3(Ce)闪烁体对能量的线性好于NaI(Tl),这预示了氯化镧[LaCl3(Ce)]闪烁体在Χ射线安检成像方面应用的巨大前景。
作为闪烁体探测器,还有一个重要的组成部件——光敏元件。现在不仅有各种各样的光电倍增管,还研发出了硅光电二极管和MCP-PMT(微通道板光电倍增管)。MCP-PMT是微通道板配以光阴极、阳极组成的光电倍增管。光阴极发射的光电子被拉进微通道板细管内,碰撞其内壁多次倍增后经阳极输出,MCP-PMT的特点是小型、坚固、增益高、时间响应快(上升时间150ps,下降时间360ps)、抗磁场干扰、功耗低。它与近几年来发展起来的晶体开槽技术,已经构成了新型的闪烁体位置灵敏探测器,明显提高了空间分辨(提高到2.1mm),提高了闪烁体探测器用于Χ、γ射线成像的排列密度。
核辐射探测半导体探测器
利用半导体来探测射线是美国贝尔电话实验室的麦凯(Mckey)在1949年首先提出的。当时他发现,用磷铜丝压在Ge半导体块上构成的耐反向高压点接触二极管,在受到放射性核素(Po)放出的α粒子照射时有脉冲输出,这说明,这种二极管可以构成射线探测器。1951年他又用Ge晶体的P-N结型二极管记录了α粒子。于是,这种探测器很快引起了世界各国的重视。
第一个用于制作核辐射探测器的半导体材料是金刚石,它在1956年就开始被用作α粒子辐射探测器。但这种材料不易获得,而且原子序数太低,能量分辨率不好,所以在1958年前后戴维斯(Davis)等人利用反向偏压的Ge、Si扩散结和面垒型P-N结构成的半导体辐射探测器后,它就被淘汰了。1960年,弗洛尔达(Foielda)等人用Si P-N结测量α粒子能谱,对5MeV的α粒子能量分辨高达0.6%(30keV),比当时所有其它的探测器的性能都好。同期便有美国、加拿大的几家公司生产了Si半导体探测器,并商品化。
1960年,迈耶(Mayer)等人利用锂离子漂移技术成功地研制成了Si(Li)探测器。1962年,半导体探测器已被用来测量电子、质子、α粒子、重离子和裂变碎片,能量分辨率也进一步得到了提高,对241Am 5.486MeV的α粒子,FWHM为22keV(0.4%)。
- 相关百科
- 相关知识
- 相关专栏
- 电磁场与电磁波第四版
- 电磁场与电磁波(第二版)
- 电磁场数值计算与仿真分析
- 电磁场重点难点及典型题精解
- 电磁安防
- 电磁屏蔽室屏蔽效能的测量方法
- 电磁屏蔽室工程技术规范 GB/T 50719―2011
- 电磁屏蔽用全方位导电海绵通用技术要求
- 电磁应用与防护手册
- 电磁弹性结构的非线性弯曲和磁弹性稳定性
- 电磁感应定向凝固离心铸造系统
- 电磁推进
- 电磁暂态程序
- 电磁桥式起重机
- 电磁气动接触器
- 电磁污染
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中国工程图学学会成立工程与制造系统集成化分会
- 可替代现有隔热保温材料的新型材料
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 中国工程造价咨询业的发展趋势
- 支持并行工程和智能CAPP的制造资源建模技术
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定
- 智能建筑工程报警与电视监控系统前端设备的安装施工

