电磁场的保角变换

数学上规定复平面和复平面之间的变换=()是导数′()厵0的各点处是保角变换,它是求解二维电磁场问题的一种有力工具。例如两个平行的柱形电极,当长度远大于间距从而可以忽略柱体的末端效应时，就可近似为二维问题。保角变换可应用于:静电、静磁问题，包括传输线(即横电磁场)问题;具有复杂边界的导波系统问题;以及电磁场的反演问题。

静电、静磁问题的应用甚广，在电源或磁源以外的区域，二维问题的电场强度或磁场强度等于某一静势函数的梯度，后者满足二维拉普拉斯方程，其解称为(圆)调和函数，记为(,)，则

设复变数=+j，则根据已知的(,),总可以找到另一个调和函数=(,)，构成解析函数

ω(z)=u+jv

z=x+jy

称和为共轭函数,为复势函数。可以证明也满足二维拉普拉斯方程并且在复平面上的等值线是两簇互相正交的曲线。若选其中的一簇为等势线，则另一簇就代表力线(电力线、磁力线)，相应地称这两簇曲线所对应的函数为势函数和流函数(通量函数)。

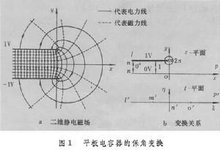
电磁场的保角变换 若能找到两个共轭函数，其中一个函数的等值线恰好和所研究的电极边界重合，则另一个函数的等值线即代表由电极发出的电力线。因而,根据电力线的流函数就可以计算出电极表面所带的电荷量，从而可以计算场分布和电容量等。例如平板电容器二维边缘场的分析(图1a)。设两极板的电位分别为±1伏，间距为2(长度单位)，置于-平面中(=+j)，根据对称性，只需分析上半平面(>0)的场。利用解析函数

的保角变换(=+j)，使-平面上由点、、连成的多角形变换成以点′、′、′连线为界的上半-平面(图1b)。已知后者的复势函数为

故平板电容器的复势函数满足关系式

据此可得出在-平面内的等势线(=常数)和电力线(=常数)的曲线方程。

某些边界形状较复杂的导波系统，经保角变换可变换成一个较易处理的简单边界形状。例如利用波导的电磁场解描述沟槽形波导(图2)的电磁场时就需要用保角变换。

电磁场的保角变换 在电磁场反演问题中，由已知远区场推算电磁场源的距离、方向和形状时，可采用保角变换，将已知二维闭合曲线的外域变换成单位圆的外域，并利用变换函数以及远区场两者的劳伦茨级数展开式的系数关系，可以得出解的低频估计。

在具体问题中，根据预给的势函数或流函数，去寻找合适的共轭函数并不容易。对于场域具有多角形边界的问题，施瓦茨变换是一种很有用的方法。它把一个复平面上由实轴和无限大的圆弧所围成的上半平面变换到另一复平面上的多角形内域，或反之。对于除了平角和零角之外只含一、二个正角的多角形，施瓦茨变换是初等解析函数;当正角增加到三、四个，变换与椭圆积分及椭圆函数有关。椭圆函数属于双周期解析函数，常应用于分析带状线等特种截面传输线。