赤水华越房地产开发有限公司
赤水华越房地产开发有限公司基本信息
| 公司名称 | 赤水华越房地产开发有限公司 | 成立时间 | 2011年02月28日 |
|---|---|---|---|
| 总部地点 | 赤水市大同镇民族村丹霞溪谷国际休闲度假区1号楼1层1号 | ||
赤水华越房地产开发有限公司造价信息
赤水华越房地产开发有限公司常见问题
-
挺好的。公司于2008年成立,是集房地产开发、销售、物业管理于一体的私营企业,我公司立足脚踏实地、稳扎稳打,历年来都是连山区纳税标兵,我们以最亲民环境,最符合民意的房价为老百姓服务,公司不求发展规模最...
-
简介:扬州越都房地产开发有限公司成立于2011年03月10日,主要经营范围为许可经营项目:房地产开发等。法定代表人:陈鼎兴成立时间:2011-03-10注册资本:1018万工商注册号:32108800...
-
天津高盛房地产开发有限公司位于天津市天津港保税区天保大道97号212室 天津高盛房地产开发有限公司公司主要经营房地产开发,销售,出租及相关咨询服务。公司拥有一批专业管理和技术人才,在行业中享有很高的声...
赤水华越房地产开发有限公司文献

 房地产开发有限公司公司章程
房地产开发有限公司公司章程
房地产开发有限责任公司 公司章程 2013 年 月 日 1 目 录 第一章 总 则 ............................................. 1 第二章 公司经营范围 ...................................... 1 第三章 公司的注册资本与实收资本 .......................... 1 第四章 股东出资 .......................................... 2 第五章 股东权利及义务 .................................... 2 第六章股东转让出资的条件 ................................. 3 第七章公司的机构及其生产办法、职权、议事规则 ............. 3 第八章公司的法定代表人

 房地产开发有限公司章程1
房地产开发有限公司章程1
1 江苏省连云港 志恒房地产开发有限公司章程 第一章 总 则 第一条 根椐《中华人民共和国公司法》 ,《中华人民共和国 登记管理条例》和国家有关法律、行政法规,制定本公司(以下 简称公司)章程。 第二条 公司宗旨是: 深化经济体制改革, 遵循市场经济规 律,以诚信为本,积极开拓市场,促进 xxxx 民营经济的大力发 展。 第三条 公司名称为:连云港 xx 房地产开发有限公司。 第四条 公司住所在: xxxx 市 xxxx 北路。 第五条 公司经营范围是:房地产经营及开发。 第六条 公司为有限责任公司, 股东以其出资额为限对公司 承担责任,公司以其全部资产对公司的债务承担责任。 第七条 公司在江苏省连云港市灌南县工商行政管理局注 册登记,公司的合法权受法律保护。 第二章 股 东 第八条 公司股东共 4个,名称与住所如下: 张磊:昆山市 2 朱作喜:江苏省宿迁市宿豫区人 何亦峰:浙江省杭州
水华是荷花的别称。
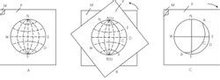
极射赤平投影赤平投影
投影原理
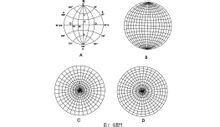
一切通过球心的面和线,延伸后均会与球面相交,并在球面上形成大圆和点。以球的北极为发射点,与球面上的大圆和点相连,将大圆和点投影到赤道平面上,这种投影称为极射赤平投影。本教材采用下半球投影,即只投影下半球的大圆弧和点。
图2为一球体,AC为垂直轴线,BD是水平的东西轴线,FP是水平的南北轴线,BFDP为过球心的水平面,即赤平面。
平面的投影方法(图2)设一平面走向南北、向东倾斜、倾角40°,若此平面过球心,则其与下半球面相交为大圆弧PGF,以A点为发射点,PGF弧在赤平面上的投影为PDF弧。PDF弧向东凸出,代表平面向东倾斜、走向南北,DH之长短代表平面的倾角。
直线的投影方法(图3)设一直线向东倾伏、倾伏角40°,此线交下半球面于G点。以A为发射点,球面上的G点在赤平面上的投影为H。HD的长短代表直线的倾伏角、D的方位角即直线的倾伏向。同理,一条直线向南西倾伏、倾伏角20°,此线交下半球面于J点,其赤平投影为K。
为了准确、迅速地作图或量度方向,可采用投影网。常用的有吴尔福网(简称吴氏网,也称等角距网)(图4A)和施密特网(等面积网)(图4B),以及据其改换形式而成的极等角度网(图4C)和极等面积网(赖特网)(图4D)。吴尔福网与施密特网基本特点相同,下面以吴尔福网为例介绍投影网。
吴尔福投影网
结构要素
基圆:即赤平面与球面的交线,是网的边缘大圆。由正北顺时针为0°-360°,每小格2°,表示方位角,如走向、倾向、倾伏向等。
两个直径 分别为南北走向和东西走向直立平面的投影。自圆心→基圆为90°→0°,每小格2°,表示倾角、倾伏角。
经线大圆:是通过球心的一系列走向南北、向东或向西倾斜的平面的投影,自南北直径向基圆代表倾角由陡到缓的倾斜平面。
纬线小圆 是一系列不通过球心的东西走向的直立平面的投影。它们将南北向直径、经线大圆和基圆等分,每小格2°。
操作
将透明纸(或透明胶片等)蒙在吴氏网上,描绘基圆及"+"字中心,固定网心,使透明纸能旋转。然后在透明纸上标上N、E、S、W。
平面的投影 标绘产状SE120°∠30°的平面(图5)。
将透明纸上的指北标记N与投影网正北重合,以北为0°,在基圆上顺时针数至120°得一点D,为平面的倾向(图6A)。
转动透明纸将D点移至东西直径上(转至南北直径也可),自D点向圆心数30°得C点,标绘C所在的经线大圆弧(图6B中之ACB),AB为平面的走向。
转动透明纸,使指北标记与投影网正北重合,ACB图5 产状120°∠30°平面的透视图大圆弧即为SE120°∠30°平面的投影(图6C)。
直线的投影
标绘产状为NW330°∠40°的直线。
使透明纸上正北标记N与投影网正北重合,以N为0°,在基圆上顺时针数至330°得一点A,为直线的倾伏向(图7A)。
把A点转至东西直径上(转至南北直径也可),由A点向圆心数40°得A´点(图7B)。
把透明纸的指北标记转至与投影网 正北重合,A´即为产状NW330°∠40°的直线的投影(图7C)。
法线的赤平投影
是指平面法线的产状标绘。法线的投影是极点,平面的投影是圆弧,二者互相垂直,夹角相差90°。往往用法线的投影代表与其相对应的平面的投影,这样较为简单。
例 求产状为E90°∠40°的平面法线的投影(图8)
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影。
某岩层产状为NW330°∠40°,求在NW335°方向剖面上该岩层的视倾角(图9)。
据岩层面产状作其投影弧EHF。在基圆上数至NW335°得D´点。
作D´点与圆心O的连线,交EHF于H´点。H´为岩层面与NW335°方向剖面的交线在下半球的投影。D´H´间的角距即为NW335°方向上的视倾角。
求两平面交线的产状(图10)
据已知的两平面产状,在吴氏网上分别求出其投影大圆弧EHF和JHK。两大圆弧的交点H即为两平面交线与下半球面交点的投影
作H与圆心O的连线,交基圆于G点,G点的方位角即两平面交线的倾伏向,GH间的角距为交线的倾伏角。
求两相交直线所决定的平面的产状
已知两相交直线的产状分别为SE120°∠36°和S180°∠20°,求其所决定的平面的产状(图11)。
据已知产状作出两直线的投影点D´、F´。
转动透明纸使D´、F´两点位于同一经线大圆弧上,AF´D´B大圆弧即为两相交直线所共平面的投影。
求平面上直线的投影 已知一平面产状S180°∠37°,该平面上一直线侧伏向E,侧伏角44°,求直线的倾伏向、倾伏角(图12)。
依平面产状作出其投影大圆弧,并标出其朝东的走向A。
将大圆弧转至SN方向,自A点数经线大圆与纬线小圆的交点,读出侧伏角44°(θ),标出该点C″,C″为直线在平面上的投影。
C″C′间的角距γ即为直线的倾伏角,C′的方位角则为直线的倾伏角。
小结
一切面状构造、如岩层面、断层面、劈理、流面、褶图12 平面上直线的投影 皱轴面等的投影方法,都可采用空间平面的投影方法。一切线状构造、如二平面的交线、走向线、倾斜线、擦痕、流线、褶皱的枢纽、轴迹等的投影方法,都与直线的投影相同。这些面状和线状构造的产状要素都可以借助于前述赤平投影的方法求得。利用这些方法可以解决以下构造问题。
1.已知岩层产状,求某一方向剖面上的岩层视倾角;
已知岩层在两剖面方向上的视倾角,求岩层的走向、倾向和倾角;
求断层面与岩层面交迹线的产状;
已知断层面产状及其上擦痕的侧伏角,求擦痕的倾伏向、倾伏角;
求一对共轭剪节理的交线(即变形椭球体的B轴)的产状。
极射赤平投影投影原理
一切通过球心的面和线,延伸后均会与球面相交,并在球面上形成大圆和点。以球的北极为发射点,与球面上的大圆和点相连,将大圆和点投影到赤道平面上,这种投影称为极射赤平投影。本教材采用下半球投影,即只投影下半球的大圆弧和点。
图2为一球体,AC为垂直轴线,BD是水平的东西轴线,FP是水平的南北轴线,BFDP为过球心的水平面,即赤平面。
平面的投影方法(图2)设一平面走向南北、向东倾斜、倾角40°,若此平面过球心,则其与下半球面相交为大圆弧PGF,以A点为发射点,PGF弧在赤平面上的投影为PHF弧。PDF弧向东凸出,代表平面向东倾斜、走向南北,DH之长短代表平面的倾角。
直线的投影方法(图3)设一直线向东倾伏、倾伏角40°,此线交下半球面于G点。以A为发射点,球面上的G点在赤平面上的投影为H。HD的长短代表直线的倾伏角、D的方位角即直线的倾伏向。同理,一条直线向南西倾伏、倾伏角20°,此线交下半球面于J点,其赤平投影为K。
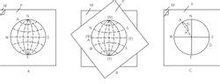
为了准确、迅速地作图或量度方向,可采用投影网。常用的有吴尔福网(简称吴氏网,也称等角距网)(图4A)和施密特网(等面积网)(图4B),以及据其改换形式而成的极等角度网(图4C)和极等面积网(赖特网)(图4D)。吴尔福网与施密特网基本特点相同,下面以吴尔福网为例介绍投影网。
极射赤平投影吴尔福投影网
结构要素
基圆:即赤平面与球面的交线,是网的边缘大圆。由正北顺时针为0°-360°,每小格2°,表示方位角,如走向、倾向、倾伏向等。
两个直径 分别为南北走向和东西走向直立平面的投影。自圆心→基圆为90°→0°,每小格2°,表示倾角、倾伏角。
经线大圆:是通过球心的一系列走向南北、向东或向西倾斜的平面的投影,自南北直径向基圆代表倾角由陡到缓的倾斜平面。
纬线小圆 是一系列不通过球心的东西走向的直立平面的投影。它们将南北向直径、经线大圆和基圆等分,每小格2°。
操作
将透明纸(或透明胶片等)蒙在吴氏网上,描绘基圆及“ ”字中心,固定网心,使透明纸能旋转。然后在透明纸上标上N、E、S、W。
平面的投影 标绘产状SE120°∠30°的平面(图5)。
将透明纸上的指北标记N与投影网正北重合,以北为0°,在基圆上顺时针数至120°得一点D,为平面的倾向(图6A)。
转动透明纸将D点移至东西直径上(转至南北直径也可),自D点向圆心数30°得C点,标绘C所在的经线大圆弧(图6B中之ACB),AB为平面的走向。
转动透明纸,使指北标记与投影网正北重合,ACB图5 产状120°∠30°平面的透视图大圆弧即为SE120°∠30°平面的投影(图6C)。
直线的投影
标绘产状为NW330°∠40°的直线。
使透明纸上正北标记N与投影网正北重合,以N为0°,在基圆上顺时针数至330°得一点A,为直线的倾伏向(图7A)。
把A点转至东西直径上(转至南北直径也可),由A点向圆心数40°得A´点(图7B)。
把透明纸的指北标记转至与投影网正北重合,A´即为产状NW330°∠40°的直线的投影(图7C)。
法线的赤平投影
是指平面法线的产状标绘。法线的投影是极点,平面的投影是圆弧,二者互相垂直,夹角相差90°。往往用法线的投影代表与其相对应的平面的投影,这样较为简单。
例 求产状为E90°∠40°的平面法线的投影(图8)
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影。
某岩层产状为NW330°∠40°,求在NW335°方向剖面上该岩层的视倾角(图9)。
据岩层面产状作其投影弧EHF。在基圆上数至NW335°得D´点。
作D´点与圆心O的连线,交EHF于H´点。H´为岩层面与NW335°方向剖面的交线在下半球的投影。D´H´间的角距即为NW335°方向上的视倾角。
求两平面交线的产状(图10)
据已知的两平面产状,在吴氏网上分别求出其投影大圆弧EHF和JHK。两大圆弧的交点H即为两平面交线与下半球面交点的投影
作H与圆心O的连线,交基圆于G点,G点的方位角即两平面交线的倾伏向,GH间的角距为交线的倾伏角。
求两相交直线所决定的平面的产状
已知两相交直线的产状分别为SE120°∠36°和S180°∠20°,求其所决定的平面的产状(图11)。
据已知产状作出两直线的投影点D´、F´。
转动透明纸使D´、F´两点位于同一经线大圆弧上,AF´D´B大圆弧即为两相交直线所共平面的投影。
求平面上直线的投影 已知一平面产状S180°∠37°,该平面上一直线侧伏向E,侧伏角44°,求直线的倾伏向、倾伏角(图12)。
依平面产状作出其投影大圆弧,并标出其朝东的走向A。
将大圆弧转至SN方向,自A点数经线大圆与纬线小圆的交点,读出侧伏角44°(θ),标出该点C″,C″为直线在平面上的投影。
C″C′间的角距γ即为直线的倾伏角,C′的方位角则为直线的倾伏角。
小结
一切面状构造、如岩层面、断层面、劈理、流面、褶图12 平面上直线的投影 皱轴面等的投影方法,都可采用空间平面的投影方法。一切线状构造、如二平面的交线、走向线、倾斜线、擦痕、流线、褶皱的枢纽、轴迹等的投影方法,都与直线的投影相同。这些面状和线状构造的产状要素都可以借助于前述赤平投影的方法求得。利用这些方法可以解决以下构造问题。
1.已知岩层产状,求某一方向剖面上的岩层视倾角;
已知岩层在两剖面方向上的视倾角,求岩层的走向、倾向和倾角;
求断层面与岩层面交迹线的产状;
已知断层面产状及其上擦痕的侧伏角,求擦痕的倾伏向、倾伏角;
求一对共轭剪节理的交线(即变形椭球体的B轴)的产状。
- 相关百科
- 相关知识
- 相关专栏
- 赤水市交通建筑建材工程有限责任公司
- 赤水市人民政府关于明确赤水市小水电站资产抵押登记部门的通知
- 赤水市人民政府关于重申财政性资金投资项目管理有关规定的通知
- 赤水市伟容建材租赁有限公司
- 赤水市住房和城乡建设局
- 赤水市农村村民建房占补平衡管理办法
- 赤水市残疾人综合服务设施、流浪未成年人救助管理中心工程招标代理公司招标公告
- 赤水市瑞丰房地产开发有限公司
- 赤水市2008年度农业综合开发土地治理项目(大同二标段)二次招标公告
- 赤苞花
- 赤迅橱柜销售设计系统
- 赫敦(无锡)金属制品有限公司
- 赫斯曼锡基轴承合金
- 赫科玛电缆(上海)有限公司
- 赫章县房屋征收与补偿安置办公室志愿服务队
- 赫英木结构制造(天津)有限公司
- 在生活中构筑自然——河南天旺园林工程有限公司剪影
- 张家港市旺达工业气体有限公司企业信用报告-天眼查
- 云南璟成工程项目管理有限公司-招投标数据分析报告
- 浙江深美装饰工程有限公司生产车间工程安全监理细则
- 中国建筑第二工程局有限公司上海公司合格供应商名录
- 一心一意谋发展 中国重型汽车集团有限公司发展纪实
- 中国水利水电第十六工程局有限公司机场施工发展战略
- 中国恩菲工程技术有限公司中国有色工程设计总院
- 永明项目管理有限公司中原分公司中标
- 以思想解放推进发展新跨越竭力打造中原建设工程铁军
- 永明项目管理有限公司西宁分公司中标
- 在听取四川省“三江”水电综合考察情况汇报时邹家华
- 中国石油天然气股份有限公司安全生产管理暂行办法
- 中国建筑装饰工程有限公司
- 环境设计专业卓越工程师培养模式探析
- 永明项目管理有限公司立远分公司中标