磁路欧姆定律定性分析
为了使较小的励磁电流产生较大的磁通,在电机、变压器以及各种铁磁元件中常用磁性材料做成一定形状的铁心。铁心的磁导率比周围空气或者其他物质的磁导率高很多,因此磁通的绝大部分经过铁心形成闭合回路,这种人为造成的磁通路径被称为磁路。图3.1-3是最为简单的磁路。
磁路欧姆定律造价信息
以图5-6所示环形铁心磁路为例,设环形铁心上的线圈是密绕的而且绕得很均匀,从而使得沿铁心中心线产生的磁场各处大小相等,并且磁场强度的方向和铁心中心线的方向一致。
根据全电流定律,有
变成为:Φ=F/Rm
式中:Rm是磁阻,是表示磁路对磁通具有阻碍作用的物理量。
F是磁动势,由它产生磁通Φ,F=IN。
Φ是磁通量,单位为韦伯。
最后化简公式在形式上与电路的欧姆定律相似,称为磁路欧姆定律,它对分析电磁元件的磁路、磁路和电路问的相互关系及运行特性等都具有较大的价值。
磁阻Rm与磁路的平均长度z成正比,与磁路的截面积S及构成磁路材料的磁导率口成反比,所以磁路磁阻的大小取决于磁路的几何尺寸和所采用材料的磁导率。磁路长度越长,截面积越小,磁阻就越大;材料的磁导率越大,磁阻越小。所以铁磁材料组成的磁路磁阻很小,即使是很小的气隙,由于其磁导率很小,其磁阻也很大。在电机的磁路中,电机气隙很小,但却是电机磁路磁阻最大的部分。值得注意的是铁磁材料的磁导率岸不是常数,所以由铁磁材料构成的磁路,其磁阻也不是常数,而是随磁路中磁通密度的大小而变化,即铁磁材料的磁路具有非线性。
磁路欧姆定律定性分析常见问题
-
1.小明家有一个标有“220V、800W”的电炉,在额定电压下用10分钟能烧开一壶水。一天他用这个电炉在相同环境下(空气的温度和压强相同)烧开同样一壶水用了12分钟,请你帮助小明算一算他家当时的电源电...
-
用ANSYS作考虑渗透压的边坡稳定分析分析,ANSYS,考虑渗透压,渗透压的,边坡的稳定,边坡稳定,边坡,边...
以应用磁路欧姆定律分析电机和电器为例说明
根据磁路欧姆定律,我们可以发现,磁路中的磁通相当于电路中的电流,磁压降(或磁势)相当于电路中的电压降(或电势),而磁阻则相当于电路中的电阻,这样,就可把磁路的问题仿照电路的问题来解决。
在运用时应注意磁路有其自身的特点。在机电设备中,不导磁的铜、不锈钢等金属材料和绝缘材料及空气隙在磁路中均描述成空气隙,它与气隙的大小δ成正比,与磁路的截面积 Sδ及其导磁率μ0成反比,它的导磁率为常数。铁磁物质的磁阻用 RFe表示,它与磁路的长度成正比,与导磁体的截面积及其导磁率成反比,它的导磁率与导磁体的物理性质及饱和程度有关,不是常数。这和电阻不完全一样。
下面用磁路欧姆定律分析一个典型的磁路问题:直流电机的主磁场
直流电机的主磁场是电机实现机电能量转换的关键。为了清楚知道电机的工作情况,必须具体分析空载时直流电机的磁场和气隙磁密的分布情况。这个问题如果用陈述性语言去分析,是非常困难的。应用磁路欧姆定律,把电机的磁场关系进行量化,便可以用数学方法去进行有关的计算和分析。
首先,根据磁路按材料和截面分段的原则,对闭合的主磁路可分为五段,即空气隙、电枢齿、电枢轭部、主磁极和定子磁轭。其中除空气隙是空气介质外,其余各段均是铁磁物质。这样,可把磁路中的磁阻分解为铁磁阻 RFe和空气隙的磁阻Rδ,且按各段磁路的连接情况,认为铁磁阻和空气隙的磁阻是串联关系,可画出其等效磁路图,如图1中(a)所示。由于气隙中的空气导磁系数比铁磁物质的导磁系数小得多,所以气隙磁阻在磁路总磁阻中占相当大的比例。为了简化计算,通常忽略铁磁物质的磁阻,等效磁路可见图1中的(b)。这样,主磁通Φ的大小决定于励磁磁势FL跟气隙磁阻Rδ的比值。
当励磁磁势恒定时,气隙各处的磁密与该处的气隙长度δ成反比。若主磁极下的气隙是均匀的,则主磁极下的气隙磁密大小相等。据此得出气隙磁密沿电枢表面气隙空间的分布波形为一平顶波。可用同样的方法求取负载时电枢磁密的分布波形。 2100433B
磁路欧姆定律定性分析文献

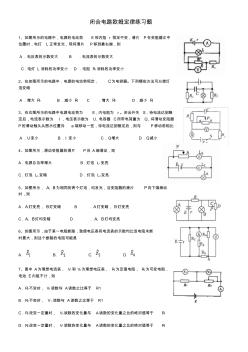 闭合电路欧姆定律-动态分析专题
闭合电路欧姆定律-动态分析专题
闭合电路欧姆定律练习题 1、如图所示的电路中,电源的电动势 E和内阻 r 恒定不变,滑片 P在变阻器正中 位置时,电灯 L正常发光,现将滑片 P移到最右端,则 A.电压表的示数变大 B .电流表的示数变大 C.电灯 L 消耗的功率变小 D .电阻 R1消耗的功率变小 2、在如图所示的电路中,电源的电动势恒定, C为电容器。下列哪些方法可以使灯 泡变暗 A.增大 R1 B.减小 R1 C .增大 R2 D.减小 R2 3、在右图所示的电路中电源电动势为 E,内电阻为 r。闭合开关 S,待电流达到稳 定后,电流表示数为 I ,电压表示数为 U,电容器 C所带电荷量为 Q,将滑动变阻器 P的滑动触头从图示位置向 a端移动一些,待电流达到稳定后,则与 P移动前相比 A.U变小 B.I 变小 C.Q增大 D.Q减小 4、如图所示,滑动变阻器的滑片 P向

 典型例题闭合电路的欧姆定律
典型例题闭合电路的欧姆定律
【典型例题】 问题 1:闭合电路的欧姆定律的基本应用问题: [考题 1]如图所示电路中,电源的总功率是 40W, 4R1 , 6R 2 ,a、b 两点 间的电压是 4.8V,电源输出的功率是 37.6W。求电源的内电阻和电动势。 [解析] 外电路是由 21 RR 与 并联再与 3R 串联组成的。 21 RR 与 并联的总电阻为 4.2 64 64 RR RR R 21 21 ab a、b 两点间的电压就是并联电路两端的电压,所以流过干路的电流为 A2A 4.2 8.4 R U I ab ab ∵ rIPPPP 2 E 出内出 ∴ 6.0 2 6.3740 I PP r 22 E 出 电动势 V20V 2 40 I P E E 变式: [考题 2]如图甲所示电路中, 10RRR 321 ,S断开时,电压表示数为 16V; S闭合时,电压表示数为 10V。若电压表可视为理想的,求: (1)电源
磁路定理即表示闭合磁路的磁动势等于各段磁路的磁势降之和,即
,其中称为第i段磁路的“磁势降”。
磁阻、磁通势和磁通量之间关系的定律。它包括磁路第一定律和磁路第二定律。
磁路第一定律通过磁路中任一结点的磁通的代数和为零。图2中的磁路有两个分支点a和b。通常将磁路的分支点称为结点,进入结点的磁通为正,离开结点的磁通为负。在结点a处作一封闭曲面S,根据磁通的连续性原理得Φ1 Φ2-Φ3=0,它表达了磁路结点上各支路磁通之间的关系。这个定律是由磁感应线的性质所决定的,磁感应线是封闭曲线,无头无尾,因此,磁路第一定律又称磁通连续定律,也称基尔霍夫第一定律。它阐明磁路中磁通量是守恒的,在磁路计算中起重要作用。
磁路第二定律磁路中的任一回路,其磁势的代数和等于各段磁位降的代数和。图2中由l1和l3组成的闭合回路,如果取它们的中心线为闭合回线,按顺时针绕行,应用全电流定律,则有N1I1=H1l1 H3l3。再取l1和l2所组成的闭合磁路,沿磁路中心线,仍按顺时针绕行,应用全电流定律,则有N1I1-N2I2=H1l1-H2l2。对于闭合回路,磁路第二定律实质上是全电流定律,而对磁路中的某一段而言,它就是磁路欧姆定律,磁路第二定律,也称基尔霍夫第二定律。它是磁路计算的重要依据。应用磁路第二定律时,各磁势和磁位降方向的确定方法为:任意选取回路的绕行方向。磁通方向和绕行方向一致时,该段的磁位降为正,反之为负;线圈中电流的方向和绕行方向符合右手螺旋定则时,线圈的磁势为正,反之为负。
磁路第二定律,在磁路计算中起重要作用。 2100433B

电机励磁方式磁路
用以激励磁路中磁通的载流线圈称为励磁线圈(或励磁绕组),励磁线圈中的电流称为励磁电流(或激磁电流)。若励磁电流为直流,磁路中的磁通是恒定的,不随时间而变化,这种磁路称为直流磁路;直流电机的磁路就属于这一类。若励磁电流为交流,磁路中的磁通随时间交变变化,这种磁路称为交流磁路;交流铁心线圈、变压器和感应电机的磁路都属于这一类。
- 相关百科
- 相关知识
- 相关专栏
- 中国对美国出口的商品结构、比较优势及其稳定性分析
- 有限元强度折减法在路基边坡稳定性分析中的应用
- 云南某二级公路牟村段滑坡稳定性分析及治理效果评价
- 基于FLAC~(3D)顺层岩质边坡开挖稳定性分析
- 基于FlAC3D强度折减法露天煤矿边坡稳定性分析
- 孤山水电站不当施工诱发滑坡重大变形险情与稳定性分析
- 基于ABAQUS降雨入渗条件下基坑边坡稳定性分析
- 基于DEM-LEM考虑裂隙扩展岩质边坡稳定性分析
- 基于赤平投影法某顺层边坡稳定性分析及加固措施
- 框架预应力锚杆边坡支护结构稳定性分析方法及其应用
- 基于强度折减法某新建隧道下穿客运专线稳定性分析
- 基于有限差分强度折减法黄延高速公路边坡稳定性分析
- 基于多级模糊综合评判法高速公路边坡稳定性分析
- 基于移动LiDAR技术山区丘陵公路边坡稳定性分析
- 基于不同本构模型复杂地层大断面隧道开挖稳定性分析
- 岩质边坡稳定性分析中岩石强度测试与试验数据的工程处理