齿轮滚刀加工直齿圆柱齿轮

（一）轮齿的受力分析

进行齿轮的强度计算时，首先要知道齿轮上所受的力，这就需要对齿轮传动作受力分析。当然，对齿轮传动进行力分析也是计算安装齿轮的轴及轴承时所必需的。

齿轮传动一般均加以润滑，啮合轮齿间的摩擦力通常很小，计算轮齿受力时，可不予考虑。

沿啮合线作用在齿面上的法向载荷Fn垂直于齿面，为了计算方便，将法向载荷Fn在节点P处分解为两个相互垂直的分力，即圆周力Ft与径向力Fr, 。由此得

Ft=2T1/d1 ； Fr=Fttanα ； Fn=Ft/cosα (a)

式中：T1—小齿轮传递的转矩，N·mm；

d1—小齿轮的节圆直径，对标准齿轮即为分度圆直径，mm；

α—啮合角，对标准齿轮，α=20°。

（二）齿根弯曲疲劳强度计算

轮齿在受载时，齿根所受的弯矩最大 ，因此齿根处的弯曲疲劳强度最弱。当轮齿在齿顶处啮合时，处于双对齿啮合区，此时弯矩的力臂虽然最大，但力并不是最大，因此弯矩并不是最大。根据分析，齿根所受的最大弯矩发生在轮齿啮合点位于单对齿啮合区最高点。因此，齿根弯曲强度也应按载荷作用于单对齿啮合区最高点来计算。由于这种算法比较复杂，通常只用于高精度的齿轮传动（如6级精度以上的齿轮传动）。

对于制造精度较低的齿轮传动（如7，8，9级精度），由于制造误差大，实际上多由在齿顶处啮合的轮齿分担较多的载荷，为便于计算，通常按全部载荷作用于齿顶来计算齿根的弯曲强度。当然，采用这样的算法，齿轮的弯曲强度比较富余。

右边动画所示为齿轮轮齿啮合时的受载情况。动画演示为齿顶受载时，轮齿根部的应力图。

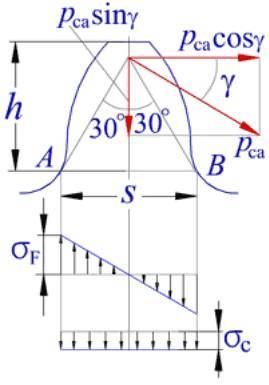
在齿根危险截面AB处的压应力σc仅为弯曲应力σF的百分之几，故可忽略，仅按水平分力pcacosγ所产生的弯矩进行弯曲强度计算。

假设轮齿为一悬臂梁，则单位齿宽（b＝1）时齿根危险截面的弯曲应力为

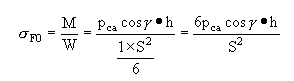
取，并将(a)式代入。对直齿圆柱齿轮，齿面上的接触线长L即为齿宽b(mm)，得

令

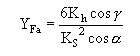
YFa是一个无量纲系数，只与齿轮的齿廓形状有关，而与齿的大小（模数m）无关。因此，称为齿形系数。S值大或h值小的齿轮，YFa的值要小些；YFa小的齿轮抗弯曲强度高。载荷作用于齿顶时的齿形系数YFa可查表查表查表查表确定。

齿根危险截面的弯曲应力为：

上式中的σF0仅为齿根危险截面处的理论弯曲应力，实际计算时，还应计入齿根危险截面处的过渡圆角所引起的应力集中作用以及弯曲应力以外的其它应力对齿根应力的影响，因而得齿根危险截面得弯曲强度条件式为

(b)

式中Ysa为载荷作用于齿顶时的应力校正系数（数值列于表<齿形系数及应力校正系数> ）。

令： φd=b/d1

φd成为齿宽系数，并将Fd=2T1/d1及m=d1/z1代入式(b),得

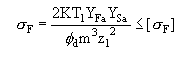
于是得

(c)

式(c)为设计计算式，式(b)为校核计算公式。

（三）齿面接触疲劳强度计算

齿面接触疲劳强度计算的基本公式为:

Fca为计算载荷,L为接触线长度,为计算方便，取接触单位长度上的计算载荷

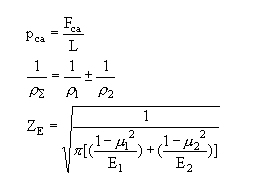
式中：ρ∑—啮合齿面上啮合点的综合曲率半径；

ZE—弹性影响系数，数值列于下表，则上式为

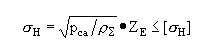
(d)

弹性影响系数ZE/()

注：表中所列夹布塑胶的泊松比μ为0.5，其余材料的μ均为0.3。

由《机械原理》得知，渐开线齿廓上各点的曲率（1/ρ）并不相同，沿工作齿廓各点所受的载荷也不一样。因此按式(d)计算齿面的接触强度时，就应同时考虑啮合点所受的载荷及综合曲率（1/ρ∑）的大小。对端面重合度

≤2的直齿轮传动，如图<齿面上的接触应力>所示，以小齿轮单对齿啮合的最低点（图中C点）产生的接触应力为最大，与小齿轮啮合的大齿轮，对应的啮合点是大齿轮单对齿啮合的最高点，位于大齿轮的齿顶面上。

如前所述，同一齿面往往齿根面先发生点蚀，然后才扩展到齿顶面，亦即齿顶面比齿根面具有较高的接触疲劳强度。因此，虽然此时接触应力大，但对大齿轮不一定会构成威胁。由图<齿面上的接触应力>可看出，大齿轮在节处的接触应力较大，同时，大齿轮单对齿啮合的最低点（图中D点）处接触应力也较大。但按单对齿啮合的最低点计算接触应力比较麻烦，并且当小齿轮齿数z1≥20时，按单对齿啮合的最低点所计算得的接触应力与按节点啮合计算得的接触应力极为相近。为计算方便，通常即以节点啮合为代表进行齿面的接触强度计算。

下面即介绍按节点啮合进行接触强度计算的方法：

节点啮合的综合曲率为

轮齿在节点啮合时，两轮齿廓曲率半径之比与两轮的直径或齿数成正比，即ρ2ρ1=d2/d1=z2/z1=u, 故得

小齿轮轮齿节点P处的 曲率半径。对于标准齿轮，节圆就是分度圆，故得 ρ1=d1sinα/2

则:

取L＝b（b为齿轮设计工作宽度）,于是(d)式为:

令

——区域系数（标准直齿轮α=20°时，ZH＝2.5），则可写为

MPa

将Ft=2T1/d1、φd=b/d1代入上式得 σH=

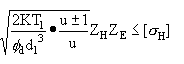
于是

mm

若将ZH＝2.5代入上面两式,得

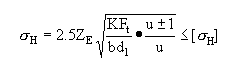
MPa

及

（四）齿轮传动的强度计算说明

按齿根弯曲疲劳强度计算时，应将

/(YFa1YSa1) 或/(YFa2YSa2)中小者代入计算。 因配对齿轮的接触应力相同，即σH1=σH2,故应将中小者代入公式进行计算。

当配对两齿轮的齿面均属硬齿面时，两轮的材料，热处理方法及硬度均可取成一样的。设计这种齿轮传动时，可分别按齿根弯曲疲劳强度及齿面接触疲劳强度的设计公式进行计算，并取其中大者作为设计结果。

当用设计公式初步计算齿轮的分度圆直径d1（或模数mn）时，动载系数Kv，齿间载荷分配系数Kα及齿向载荷分布系数Kβ不能预先确定，此时可选一载荷系数Kt(脚标t表示试选或试算值)(如取Kt=1.2～1.4)，则算出来的分度圆直径（或模数）也是一个试算值的d1t（或mnt）,然后按d1t值计算齿轮的圆周速度，查取动载系数Kv，齿间载荷分配系数Kα，及齿向载荷分布系数Kβ，计算载荷系数K。若算得的K值与试选的Kt值相差不多，就不必修改原计算；若二者相差较大时，应按下式校正试算所得分度圆直径d1t（或mnt）：

（来源：机械工业）

END