赤才
赤才,为无患子科赤才属下的一个种。灌木或乔木,高2-7米;小枝略具条纹,密被锈色绒毛。
赤才基本信息
| 中文名称 | 赤才 | 拉丁学名 | Lepisanthes rubiginosa (Roxb.) Leenh. |
|---|---|---|---|
| 二名法 | Lepisanthes rubiginosa | 界 | 植物界 |
| 门 | 被子植物门 | 纲 | 双子叶植物纲 |
| 亚纲 | 原始花被亚纲 | 目 | 无患子目 |
| 科 | 无患子科 | 亚科 | 无患子亚科 |
| 属 | 赤才属 | 分布区域 | 海南省, 广东省, 广西自治区 |
产广东、广西(西南),云南西双版纳引种。分布印度,马来半岛经中南半岛至菲律宾,南至大洋洲西北部。
赤才造价信息

赤才形态特征
常绿灌木或小乔木,高通常2-3米,有时达7米,树皮暗褐色,不规则纵裂;嫩枝、花序和叶轴均密被锈色绒毛。叶连柄长15-50厘米;小叶2-8对,革质,第一对 (近基) 卵形,明显较小,向上渐大,椭圆状卵形至长椭圆形,长3-20厘米,顶端钝或圆,很少短尖,全缘,腹面深绿色,稍有光泽,仅中脉和侧脉上有毛,背面干时常变褐色,被绒毛,毛通常很密,很少稀疏;侧脉约10对,末端不达叶缘;小叶柄粗短,长常不及5毫米。花序通常为复总状,只有一回分枝,分枝的上部密花,下部疏花;苞片钻形;花芳香,直径约5毫米;萼片近圆形,长2-2.5毫米;花瓣倒卵形,长约5毫米;花丝被长柔毛。果的发育果爿长12-14毫米,宽5-7毫米,红色。花期春季,果期夏季。
赤才常见问题
-
赤榆木价格是175元,榆木木性坚韧,纹理通达清晰,硬度与强度适中,一般透雕浮雕均能适应,刨面光滑,弦面花纹美丽,有“鸡翅木”的花纹,是主要家具用材之一。其木材的特征,心边材区分明显,边材窄暗黄色,心材...
-
小森林禁止捉一切宠,同样的有雪拉比的迷宫; 又一个好东西让我找到了,慢慢看吧: 许愿之洞,71-75,你检查一下; 不是,这是全怪兽的出现位置,有些进化过的不能捉。 ハガネやま(钢铁山),共9层 烈雀...
-
2013年10月30日,郴州赤石特大桥迎来历史性时刻-4个主塔全面封顶。由国内顶尖桥梁建设队伍中交二航局和中铁大桥局承建,赤石特大桥于2010年3月28日开工建设,2014年底建成通车。
赤才文献

 “柔性”引才研究“柔性”引才研究
“柔性”引才研究“柔性”引才研究
“柔性”引才研究“柔性”引才研究 [摘要 ]金山区作为上海市郊制造业基地, “柔性”引才已成为人才引进的一种 重要方式,这与金山区区情以及人才需求结构是密切相关的。 通过对上海金山区 的实地调研、访谈以及相关案例研究, 对上海市郊制造业基地 ——金山区“柔性” 引才在主体、岗位类别、形式、来源、途径等方面的特征和存在的问题进行实证 分析,建议从完善人才引进机制、创建平台、引进与培养并重、营造环境等方面 来健全、完善 “柔性”引才。 [关键词 ]柔性引才;不平衡;机制;平台;环境 人才是兴国之本、富民之基、发展之源,是科技创新、经济发展、社会进步 的探索者、实践者、推进者。作为上海市郊的金山区,随着 “杭州湾北岸先进制 造业基地 ”的定位以及产业结构的进一步优化,目前已确立了八大先进制造业产 业集群的发展格局。这些特殊的区情使得金山区对先进制造业人才和科技创新型 人才的需求越来越迫切。 人才

 低温拜耳法赤泥回收铝、钠工艺研究(赤泥烧结)
低温拜耳法赤泥回收铝、钠工艺研究(赤泥烧结)
低温拜耳法赤泥回收铝、钠工艺研究(赤泥烧结)
生长于潮湿山谷中。
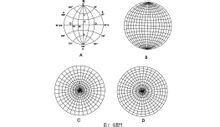
极射赤平投影赤平投影
投影原理
一切通过球心的面和线,延伸后均会与球面相交,并在球面上形成大圆和点。以球的北极为发射点,与球面上的大圆和点相连,将大圆和点投影到赤道平面上,这种投影称为极射赤平投影。本教材采用下半球投影,即只投影下半球的大圆弧和点。
图2为一球体,AC为垂直轴线,BD是水平的东西轴线,FP是水平的南北轴线,BFDP为过球心的水平面,即赤平面。
平面的投影方法(图2)设一平面走向南北、向东倾斜、倾角40°,若此平面过球心,则其与下半球面相交为大圆弧PGF,以A点为发射点,PGF弧在赤平面上的投影为PDF弧。PDF弧向东凸出,代表平面向东倾斜、走向南北,DH之长短代表平面的倾角。
直线的投影方法(图3)设一直线向东倾伏、倾伏角40°,此线交下半球面于G点。以A为发射点,球面上的G点在赤平面上的投影为H。HD的长短代表直线的倾伏角、D的方位角即直线的倾伏向。同理,一条直线向南西倾伏、倾伏角20°,此线交下半球面于J点,其赤平投影为K。
为了准确、迅速地作图或量度方向,可采用投影网。常用的有吴尔福网(简称吴氏网,也称等角距网)(图4A)和施密特网(等面积网)(图4B),以及据其改换形式而成的极等角度网(图4C)和极等面积网(赖特网)(图4D)。吴尔福网与施密特网基本特点相同,下面以吴尔福网为例介绍投影网。
吴尔福投影网
结构要素
基圆:即赤平面与球面的交线,是网的边缘大圆。由正北顺时针为0°-360°,每小格2°,表示方位角,如走向、倾向、倾伏向等。
两个直径 分别为南北走向和东西走向直立平面的投影。自圆心→基圆为90°→0°,每小格2°,表示倾角、倾伏角。
经线大圆:是通过球心的一系列走向南北、向东或向西倾斜的平面的投影,自南北直径向基圆代表倾角由陡到缓的倾斜平面。
纬线小圆 是一系列不通过球心的东西走向的直立平面的投影。它们将南北向直径、经线大圆和基圆等分,每小格2°。
操作
将透明纸(或透明胶片等)蒙在吴氏网上,描绘基圆及"+"字中心,固定网心,使透明纸能旋转。然后在透明纸上标上N、E、S、W。
平面的投影 标绘产状SE120°∠30°的平面(图5)。
将透明纸上的指北标记N与投影网正北重合,以北为0°,在基圆上顺时针数至120°得一点D,为平面的倾向(图6A)。
转动透明纸将D点移至东西直径上(转至南北直径也可),自D点向圆心数30°得C点,标绘C所在的经线大圆弧(图6B中之ACB),AB为平面的走向。
转动透明纸,使指北标记与投影网正北重合,ACB图5 产状120°∠30°平面的透视图大圆弧即为SE120°∠30°平面的投影(图6C)。
直线的投影
标绘产状为NW330°∠40°的直线。
使透明纸上正北标记N与投影网正北重合,以N为0°,在基圆上顺时针数至330°得一点A,为直线的倾伏向(图7A)。
把A点转至东西直径上(转至南北直径也可),由A点向圆心数40°得A´点(图7B)。
把透明纸的指北标记转至与投影网 正北重合,A´即为产状NW330°∠40°的直线的投影(图7C)。
法线的赤平投影
是指平面法线的产状标绘。法线的投影是极点,平面的投影是圆弧,二者互相垂直,夹角相差90°。往往用法线的投影代表与其相对应的平面的投影,这样较为简单。
例 求产状为E90°∠40°的平面法线的投影(图8)
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影。
某岩层产状为NW330°∠40°,求在NW335°方向剖面上该岩层的视倾角(图9)。
据岩层面产状作其投影弧EHF。在基圆上数至NW335°得D´点。
作D´点与圆心O的连线,交EHF于H´点。H´为岩层面与NW335°方向剖面的交线在下半球的投影。D´H´间的角距即为NW335°方向上的视倾角。
求两平面交线的产状(图10)
据已知的两平面产状,在吴氏网上分别求出其投影大圆弧EHF和JHK。两大圆弧的交点H即为两平面交线与下半球面交点的投影
作H与圆心O的连线,交基圆于G点,G点的方位角即两平面交线的倾伏向,GH间的角距为交线的倾伏角。
求两相交直线所决定的平面的产状
已知两相交直线的产状分别为SE120°∠36°和S180°∠20°,求其所决定的平面的产状(图11)。
据已知产状作出两直线的投影点D´、F´。
转动透明纸使D´、F´两点位于同一经线大圆弧上,AF´D´B大圆弧即为两相交直线所共平面的投影。
求平面上直线的投影 已知一平面产状S180°∠37°,该平面上一直线侧伏向E,侧伏角44°,求直线的倾伏向、倾伏角(图12)。
依平面产状作出其投影大圆弧,并标出其朝东的走向A。
将大圆弧转至SN方向,自A点数经线大圆与纬线小圆的交点,读出侧伏角44°(θ),标出该点C″,C″为直线在平面上的投影。
C″C′间的角距γ即为直线的倾伏角,C′的方位角则为直线的倾伏角。
小结
一切面状构造、如岩层面、断层面、劈理、流面、褶图12 平面上直线的投影 皱轴面等的投影方法,都可采用空间平面的投影方法。一切线状构造、如二平面的交线、走向线、倾斜线、擦痕、流线、褶皱的枢纽、轴迹等的投影方法,都与直线的投影相同。这些面状和线状构造的产状要素都可以借助于前述赤平投影的方法求得。利用这些方法可以解决以下构造问题。
1.已知岩层产状,求某一方向剖面上的岩层视倾角;
已知岩层在两剖面方向上的视倾角,求岩层的走向、倾向和倾角;
求断层面与岩层面交迹线的产状;
已知断层面产状及其上擦痕的侧伏角,求擦痕的倾伏向、倾伏角;
求一对共轭剪节理的交线(即变形椭球体的B轴)的产状。
极射赤平投影投影原理
一切通过球心的面和线,延伸后均会与球面相交,并在球面上形成大圆和点。以球的北极为发射点,与球面上的大圆和点相连,将大圆和点投影到赤道平面上,这种投影称为极射赤平投影。本教材采用下半球投影,即只投影下半球的大圆弧和点。
图2为一球体,AC为垂直轴线,BD是水平的东西轴线,FP是水平的南北轴线,BFDP为过球心的水平面,即赤平面。
平面的投影方法(图2)设一平面走向南北、向东倾斜、倾角40°,若此平面过球心,则其与下半球面相交为大圆弧PGF,以A点为发射点,PGF弧在赤平面上的投影为PHF弧。PDF弧向东凸出,代表平面向东倾斜、走向南北,DH之长短代表平面的倾角。
直线的投影方法(图3)设一直线向东倾伏、倾伏角40°,此线交下半球面于G点。以A为发射点,球面上的G点在赤平面上的投影为H。HD的长短代表直线的倾伏角、D的方位角即直线的倾伏向。同理,一条直线向南西倾伏、倾伏角20°,此线交下半球面于J点,其赤平投影为K。
为了准确、迅速地作图或量度方向,可采用投影网。常用的有吴尔福网(简称吴氏网,也称等角距网)(图4A)和施密特网(等面积网)(图4B),以及据其改换形式而成的极等角度网(图4C)和极等面积网(赖特网)(图4D)。吴尔福网与施密特网基本特点相同,下面以吴尔福网为例介绍投影网。
极射赤平投影吴尔福投影网
结构要素
基圆:即赤平面与球面的交线,是网的边缘大圆。由正北顺时针为0°-360°,每小格2°,表示方位角,如走向、倾向、倾伏向等。
两个直径 分别为南北走向和东西走向直立平面的投影。自圆心→基圆为90°→0°,每小格2°,表示倾角、倾伏角。
经线大圆:是通过球心的一系列走向南北、向东或向西倾斜的平面的投影,自南北直径向基圆代表倾角由陡到缓的倾斜平面。
纬线小圆 是一系列不通过球心的东西走向的直立平面的投影。它们将南北向直径、经线大圆和基圆等分,每小格2°。
操作
将透明纸(或透明胶片等)蒙在吴氏网上,描绘基圆及“ ”字中心,固定网心,使透明纸能旋转。然后在透明纸上标上N、E、S、W。
平面的投影 标绘产状SE120°∠30°的平面(图5)。
将透明纸上的指北标记N与投影网正北重合,以北为0°,在基圆上顺时针数至120°得一点D,为平面的倾向(图6A)。
转动透明纸将D点移至东西直径上(转至南北直径也可),自D点向圆心数30°得C点,标绘C所在的经线大圆弧(图6B中之ACB),AB为平面的走向。
转动透明纸,使指北标记与投影网正北重合,ACB图5 产状120°∠30°平面的透视图大圆弧即为SE120°∠30°平面的投影(图6C)。
直线的投影
标绘产状为NW330°∠40°的直线。
使透明纸上正北标记N与投影网正北重合,以N为0°,在基圆上顺时针数至330°得一点A,为直线的倾伏向(图7A)。
把A点转至东西直径上(转至南北直径也可),由A点向圆心数40°得A´点(图7B)。
把透明纸的指北标记转至与投影网正北重合,A´即为产状NW330°∠40°的直线的投影(图7C)。
法线的赤平投影
是指平面法线的产状标绘。法线的投影是极点,平面的投影是圆弧,二者互相垂直,夹角相差90°。往往用法线的投影代表与其相对应的平面的投影,这样较为简单。
例 求产状为E90°∠40°的平面法线的投影(图8)
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影
标绘出产状90°∠40°的平面投影大圆弧,自该平面倾斜线投影D´点在东西向直径上数90°,显然已越过圆心进入相反倾向,得P´点,该点即为产状90°∠40°平面的法线投影-极点。
也可自圆心向反倾向数40°,即得法线投影。
某岩层产状为NW330°∠40°,求在NW335°方向剖面上该岩层的视倾角(图9)。
据岩层面产状作其投影弧EHF。在基圆上数至NW335°得D´点。
作D´点与圆心O的连线,交EHF于H´点。H´为岩层面与NW335°方向剖面的交线在下半球的投影。D´H´间的角距即为NW335°方向上的视倾角。
求两平面交线的产状(图10)
据已知的两平面产状,在吴氏网上分别求出其投影大圆弧EHF和JHK。两大圆弧的交点H即为两平面交线与下半球面交点的投影
作H与圆心O的连线,交基圆于G点,G点的方位角即两平面交线的倾伏向,GH间的角距为交线的倾伏角。
求两相交直线所决定的平面的产状
已知两相交直线的产状分别为SE120°∠36°和S180°∠20°,求其所决定的平面的产状(图11)。
据已知产状作出两直线的投影点D´、F´。
转动透明纸使D´、F´两点位于同一经线大圆弧上,AF´D´B大圆弧即为两相交直线所共平面的投影。
求平面上直线的投影 已知一平面产状S180°∠37°,该平面上一直线侧伏向E,侧伏角44°,求直线的倾伏向、倾伏角(图12)。
依平面产状作出其投影大圆弧,并标出其朝东的走向A。
将大圆弧转至SN方向,自A点数经线大圆与纬线小圆的交点,读出侧伏角44°(θ),标出该点C″,C″为直线在平面上的投影。
C″C′间的角距γ即为直线的倾伏角,C′的方位角则为直线的倾伏角。
小结
一切面状构造、如岩层面、断层面、劈理、流面、褶图12 平面上直线的投影 皱轴面等的投影方法,都可采用空间平面的投影方法。一切线状构造、如二平面的交线、走向线、倾斜线、擦痕、流线、褶皱的枢纽、轴迹等的投影方法,都与直线的投影相同。这些面状和线状构造的产状要素都可以借助于前述赤平投影的方法求得。利用这些方法可以解决以下构造问题。
1.已知岩层产状,求某一方向剖面上的岩层视倾角;
已知岩层在两剖面方向上的视倾角,求岩层的走向、倾向和倾角;
求断层面与岩层面交迹线的产状;
已知断层面产状及其上擦痕的侧伏角,求擦痕的倾伏向、倾伏角;
求一对共轭剪节理的交线(即变形椭球体的B轴)的产状。
- 相关百科
- 相关知识
- 相关专栏
- 太阳花8500GT256MBDDR3
- 太阳花幻影FX5200Ultra
- 太阳花钛子6600GT
- 太阳花钛子7300GT豪华版
- 太阳花钛子7900GTX
- 太阳花钛子7300GT无极变速
- 赛木患
- 太阳花TNT2/32M
- 山青木
- 太阳花TNT2 M64/32M
- 海南柄果木
- 太阳花TF-918A
- 太阳花幻影S1800
- 太阳花化石
- 太阳花7900GS
- 太阳花8600GT128MDDR3
- 基才网络控制中央空调运行管理、控制与分户计费系统
- 基于赤平投影法某顺层边坡稳定性分析及加固措施
- 小箱梁预制场施工方案中部灌溉渠及赤洲河
- 赤泥尾矿堆场二线工程防渗层分项工程监理实施细则
- 正在执行的江苏省工程建设地方标准目录一才
- 基才作业链的目标成本管理在产品设计及战略定价中的运用
- 赤岭隧道初期支护及二次衬砌施工情况介绍
- 赤岭隧道初期支护及二次衬砌施工情况介绍资料
- 水压致裂地应力测量在福宁高速公路赤岭隧道工程中的应用
- 仁赤15标隧道不良地质专项施工方案及应急预案
- 工程学院本科生英才工程资助计划实施方案
- 关才家居空间设计项目化教学考核评价体系
- 副省长杨庆才到白城、松原检查水利工程建设情况
- 一级建造师顾永才管理要点
- 低温拜耳法赤泥回收铝、钠工艺赤泥烧结
- 四川省信息通信行业火才培养及评价工作会议召开