超静定
超静定基本信息
| 中文名 | 超静定结构 | 外文名 | complex super-statical determinate structure |
|---|---|---|---|
| 应 用 | 材料力学 | 有 关 | 实际工程 |
| 确定方法 | 静力学平衡方程 | 涉 及 | 外部约束力 |
解除超静定结构的某些约束后得到的静定结构,称为原超静定结构的基本静定系。
超静定造价信息
超静定外超
在静定结构的基础上附件“多余约束”而成的,由于涉及的全部是外部约束力,因而这种超静定结构成为外超静定结构。
超静定内超
工程还有一些结构,虽然可以用平衡方程确定全部外约束力,却不能确定其全部内力分量,这种结构称为内静定结构。
首先判断其外超静定次数,再判断内超静定次数,二者之和为系统的总超静定次数。
超静定常见问题
-
区别在于约束个数,材料力学里,一般固定端约束为三次约束,一个固定铰支座为一次约束,一个活动铰支座为一次约束。相对一个杆件而言,三个约束就足够保持平衡,称为静定结构。而超过了三个约束,就称为超静定。当约...
-
简单的定义就是,静定结构的自由度数量和约束数量相等,超静定结构是约束数量大于自由度数量。也就是说,静定结构只要有一个约束出现故障失效,那么整个结构就成为可变结构了。而超静定有多余的约束,个别约束失效了...
-
从几何构造分析的角度看,结构必须是几何不变体系。根据多余约束 n ,几何不变体系又分为: 有多余约束( n > 0)的几何不变体系——超静定结构; 无多余约束( n = 0)的几何不变体系——静...
对于静定结构 , 若其中某一构件 失效 , 则会导致整体失 效 , 因而可看作串联系 统 , 但对于超静定复杂结构 , 即非简单 串联系 统 , 又非简 单并 联 系 统 , 为此 较 准 确计 算超 静定 结 构整 休 可 靠 度 ,除应用 有限 元 分 析方法 外 , 同时引人了模糊综合评判 理 论 , 在工 程 数理 统计理 论及应 力一强 度干 涉模 型 基 础之 上 , 初步探讨了多种失效模式下 , 复杂超静定结构系统 (包括平面和 空 间衡架或刚架 ) 的可靠性析方法 。2100433B
超静定结构的一种解法为力法。
力法:解超静定系统时,可以取未知的多余约束力为基本未知量,而将变形或位移表示为未知力的函数,从而解除多余约束力,这种方法称为力法
由于多余约束的存在,使得该类结构在部分约束或连接失效后仍可以承担外荷载,但需要注意的是,此时的超静定结构的受力状态与以前是大不一样的,如果需要的话,要重新核算。求解任何超静定问题,都必须综合考虑以下三个方面的条件:(1)平衡条件。即结构的整体及任何一部分的受力状态都应满足平衡方程。(2)几何条件。也称为变形条件或位移条件、协调条件、相容条件等,即结构的变形和位移条件必须符合支承约束条件和各部分之间的变形连续条件。(3)物理条件。即变形或位移与力之间的物理关系。
在基本静定系上,除原有载荷外,还应该用相应的多余约束力代替被解除的多余约束,在载荷和多余约束作用下的基本静定系统称为相当系统
超静定文献

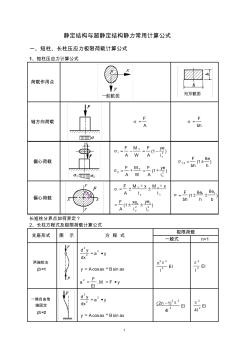 静定结构与超静定结构静力计算公式
静定结构与超静定结构静力计算公式
1 静定结构与超静定结构静力常用计算公式 一、短柱、长柱压应力极限荷载计算公式 1、短柱压应力计算公式 荷载作用点 轴方向荷载 A F bh F 偏心荷载 )1( 21 x Y i ye A F W M A F )1( 22 x Y i ye A F W M A F ) 6 1(2,1 h e bh F 偏心荷载 )1( 22 x y y x x x y Y i ye i xe A F I xM I xM A F ) 66 1( b e h e bh F yx 长短柱分界点如何界定? 2、长柱方程式及极限荷载计算公式 支座形式 图 示 方 程 式 极限荷载 一般式 n=1 两端铰支 β=1 ya dx yd 2 2 2 axBaxAy sincos yFM EI F a ,2 EI l n 2 22 EI l 2 2 一端自由他 端固定 β=2 ya dx yd 2 2 2 axB

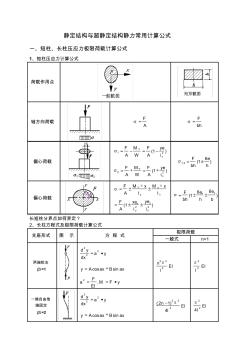 1、静定结构与超静定结构静力计算公式
1、静定结构与超静定结构静力计算公式
静定结构与超静定结构静力常用计算公式 一、短柱、长柱压应力极限荷载计算公式 1、短柱压应力计算公式 荷载作用点 轴方向荷载 A F bh F 偏心荷载 )1( 21 x Y i ye A F W M A F )1( 22 x Y i ye A F W M A F ) 6 1(2,1 h e bh F 偏心荷载 )1( 22 x y y x x x y Y i ye i xe A F I xM I xM A F ) 66 1( b e h e bh F yx 长短柱分界点如何界定? 2、长柱方程式及极限荷载计算公式 支座形式 图 示 方 程 式 极限荷载 一般式 n=1 两端铰支 β=1 ya dx yd 2 2 2 axBaxAy sincos yFM EI F a ,2 EI l n 2 22 EI l 2 2 一端自由他 端固定 β=2 ya dx yd 2 2 2 axBaxA
静定与超静定问题(statically determinate andstatically indeterminate)力系平衡时,未知数(包括未知力的大小、方向或物体的平衡位置)数目与平衡方程的数目相等时,可由静力学平衡方程求出全部未知数,称为静力学可定问题或静定问题。如果未知数数目大于平衡方程数,则不能通过平衡方程解出全部未知数,称为静力学不定问题、静不定问题或超静定问题。
求解超静定问题需要用到材料力学知识。
钱令希等的《超静定与静定结构学》分两卷,分别包括《超静定结构学》与《静定结构学》两本书的内容。上卷内容包括:绪论;结构形变;超静定结构一般性分析法;连续梁与刚构;刚构房屋之分析;桁架次应力;柱比法及变梁常数;拱;连续拱;空腹桁架;余能理论。下卷内容包括:总论;结构稳定性的研究;静定梁结构;静定桁架结构;静定拱型结构;静定立体桁架结构。
《超静定与静定结构学》可供工程设计和科学研究人员使用,也可供有关高等院校师生参考。
上卷序
下卷序
上卷 超静定结构学
第一章 绪论
1-1 结构平衡条件
1-2 静定与超静定结构
1-3 超静定结构分析之基本概念
1-4 超静定结构若干特质
1-5 超静定次数
第二章 结构形变
第三章 超静定结构一般性分析法
第四章 连续梁与刚构
第五章 刚构房屋之分析
第六章 桁架次应力
第七章 柱比法及变梁常数
第八章 拱
第九章 连续拱
第十章 空腹桁架
第十一章 余能理论
参考资料
下卷 静定结构学
第十二章 总论
第十三章 结构稳定性的研究
第十四章 静定梁结构
第十五章 静定桁架结构
第十六章 静定拱型结构
第十七章 静定立体桁架结构2100433B
- 相关百科
- 相关知识
- 相关专栏
- 超静水压力
- 超高人气墙设计沙发背景墙
- 超高分子助凝剂
- 超高功率电弧炉用镁碳砖
- 超高压交流输电工程
- 超高压容器设计
- 超高压容器
- 《超高压容器》
- 超高压技术
- 超高压杀菌
- 超高压杀菌设备
- 超高压水射流粉碎废旧轮胎制取精细胶粉理论基础研究
- 超高压水雾化
- 超高压物理改性系统
- 超高压电缆成套试验装置的建立
- 超高压电网用磁光式电流互感器的应用基础研究
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定
- 防盗门装进门洞打六根膨胀螺丝固定
- 云南省昆明市建设局建筑工程深基坑施工安全管理规定
- 园林绿化技术资料钢结构油漆分项工程质量检验评定表
- 中国石化北京设计院标准工艺装置管道垫片选用规定
- 定征复合板材粘接层性质的非线性超声兰姆波方法
- 招标控制价管理规定【辽住建发(2012)27号】
- 制度流程管理规定发布、作废、制定、审核、批准
- 整流变压器技术规格书(2016.7.5定稿)资料
- 执行新颁公路基本建设概、预算编制办法及定额的体会
- 云南某水电站水库一期蓄水安全鉴定工程施工自检报告
- 园林绿化技术资料仿古混凝土分项工程质量检验评定表
- 圆管涵、盖板涵分项工程质量检验评定表共99页文档
- 振动击实成型法水泥稳定碎石的配合比设计与施工技术
- 执勤防御(护)性器械和报警、通讯设备使用管理规定
- 新型空间梁单元及其在梁杆结构稳定分析中的应用