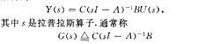
传递函数矩阵概述
传递函数矩阵(transfer function matrix)线性定常系统的一种频域描述方法.给定线性定常系统}(A,B,C).设x(0) = 0,如果记状态x(t),控制 u(t)和输出y(t)的拉普拉斯变换分别为X(s),U(s) 和Y(s),对状态方程和输出方程两边进行拉氏变换后得到
其中,是拉普拉斯算子.通常称
为系统乏的传递函数矩阵.G (s)是以:的有理分式为元素的mX:矩阵.传递函数矩阵G(s)是线性定常控制系统的另外一种描述方法.它是用频域方法分析和设计控制系统的基础.
传递函数矩阵造价信息
传递函数矩阵常见问题
-
现在市场的价格战太离谱了,导致很多的商家都必须用低价来吸引客户,所以产品质量往往都得不到保障。力弘(LHLEEHAM)提供全系列会议视听系统矩阵切换控制器,包含产品有同轴矩阵系列AHD/TVI...
-
传递函数是系统的物理参数,也就是它受硬件决定,不会随着输入变化而变化,而频率响应函数受输入参数影响。频率响应函数简称频响函数。为互功率谱函数除以自功率谱函数得到的商。频响函数是复函数,它是被测系统的动...
-
楼上恐怕还是不大了解,数字矩阵首先信号是数字信号,数字信号包括:SDI(标清)、HD-SDI(高清)这两种以前都是广播级信号,都是在广播电视应用的,但是现在随着电视会议的发展,已经出现高清电视会议系统...
传递函数矩阵文献

 矩阵函数和函数矩阵
矩阵函数和函数矩阵
矩阵函数求导 首先要区分两个概念:矩阵函数和函数矩阵 (1) 函数矩阵 ,简单地说就是多个一般函数的阵列, 包括单变量和多变量函数。 函数矩阵的求导和积分是作用在各个矩阵元素上,没有更多的规则。 单变量函数矩阵的微分与积分 考虑实变量 t 的实函数矩阵 ( )( ) ( )ij m nX t x t ×= ,所有分量函数 ( )ijx t 定义域相同。 定义函数矩阵的微分与积分 0 0 ( ) ( ) , ( ) ( ) . t t ij ijt t d d X t x t X d x d dx dx τ τ τ τ ? ? ? ??? ???= =? ??? ?? ?? ? ?? ?∫ ∫ 函数矩阵的微分有以下性质: (1) ( )( ) ( ) ( ) ( )d d dX t Y t X t Y t dt dt dt + = + ; (2) ( ) ( ) ( )( ) ( ) ( )

 矩阵
矩阵
第五章 矩 阵 §5.1 矩阵的运算 1.计算 421 421 421 963 642 321 ; 412 503 310 231 4102 2013 ; n n b b b aaa 2 1 21 ,,, ; n n bbb a a a ,, 21 2 1 ; 113 210 121 121 011 132 113 210 121 . 2.证明,两个矩阵 A 与 B 的乘积 AB 的第 i 行等于 A 的第 i 行右乘以 B, 第 j 列等于 B的第 j 列左乘以 A. 3.可以按下列步骤证明矩阵的乘法满足结合律: (i) 设 B=( ijb )是一个 n p矩阵.令 j = njj bjbb ,,2,1 是 B的第 j 列, j=1,2,⋯ ,p. 又 设 pxxx ,,, 21 是 任 意 一 个 p 1 矩 阵 . 证 明 : B = ppxxx 211 . (ii)设 A 是一个
前言
第1章 线性系统的数学描述
1.1 系统的输入一输出描述
1.1.1 基本概念
1.1.2 线性松弛系统的脉冲响应
1.1.3 具有因果性线性松弛系统的输入-输出描述
1.1.4 系统的传递函数矩阵
1.2 状态变量描述
1.2.1 状态变量与动态方程
1.2.2 齐次状态方程的解
1.2.3 非齐次状态方程的解
1.2.4 时不变系统的解
1.2.5 动态方程的等价
1.3 传递函数矩阵和矩阵分式描述
1.3.1 传递函数矩阵描述
1.3.2 传递函数矩阵的史密斯一麦克米伦形
1.3.3 矩阵分式描述
1.3.4 传递函数矩阵的零、极点
1.4 微分算子描述
1.4.1 系统矩阵
1.4.2 系统的零、极点
参考文献
第2章 线性系统的可控性和可观测性
2.1 线性系统的可控性
2.1.1 可控性的基本含义和直观例子
2.1.2 可控性的定义
2.1.3 时间函数向量的线性无关性
2.1.4 线性时变系统的可控性判据
2.1.5 线性定常系统的可控性判据
2.1.6 线性定常系统的可控性指数
2.2 线性系统的可观测性
2.2.1 可观测的基本含义和直观例子
2.2.2 可观测性的定义
2.2.3 线性时变系统的可观测性判据
2.2.4 线性定常系统的可观测性判据
2.2.5 线性定常系统的可观测性指数
2.3 线性定常系统可控、可观测的其他判据
2.3.1 Jordan形动态方程的可控性和可观测性
2.3.2 可控、可观测的几何判据
2.4 线性系统的输出可控性和输入可观测性
2.4.1 输出可控性
2.4.2 输出函数可控性
2.4.3 输入函数可观测性
2.5 线性时变系统的一致可控性和一致可观测性
2.5.1 一致可控性
2.5.2 一致可观测性
2.6 线性系统的对偶原理
2.6.1 线性时变系统的对偶原理
2.6.2 线性定常系统的对偶原理
2.7 线性系统的结构分解
2.7.1 线性时变系统在非奇异变换下的可控性和可观测性
2.7.2 线性定常系统的可控性结构分解
2.7.3 线性定常系统的可观测性结构分解
2.7.4 线性定常系统结构的规范分解
参考文献
第3章 线性定常系统的标准形和实现
3.1 单变量系统的标准形
3.1.1 可控标准形
3.1.2 可观测标准形
3.2 多变量系统的标准形
3.2.1 龙伯格第一可控标准形
3.2.2 龙伯格可观测标准形
3.2.3 块三角标准形
3.3 实现的基本概念和性质
3.3.1 基本概念
3.3.2 传递函数矩阵的可实现性
3.3.3 最小实现的特点
3.4 可控性、可观测性的频域形式
3.4.1 传递函数的可控性和可观测性
3.4.2 传递函数矩阵的可控性和可观测性
3.5 传递函数和传递函数矩阵的最小实现
3.5.1 传递函数的最小实现
3.5.2 传递函数矩阵的最小实现
3.5.3 最小实现的汉克尔矩阵法
参考文献
第4章 线性系统的稳定性
4.1 稳定性的基本概念和定理
4.1.1 稳定性的基本概念
4.1.2 李雅普诺夫第二法的主要定理
4.2 线性时变系统的稳定性判据
4.2.1 线性时变系统稳定的特点
4.2.2 线性时变系统稳定性的两个定理
4.2.3 线性时变系统的李雅普诺夫函数
4.3 线性定常系统的稳定性判据
4.3.1 基本定理
4.3.2 线性定常系统的李雅普诺夫函数
4.3.3 李雅普诺夫第二法在系统综合方面的应用
4.4 线性系统的BIBO稳定性和BIBS稳定性
4.4.1 线性时变系统的BIBO稳定性
4.4.2 线性定常系统的BIBO稳定性
4.4.3 线性系统的BIBS稳定性和总体稳定
参考文献
第5章 线性系统时域中的反馈控制与综合
5.1 状态反馈的特征配置
5.1.1 状态反馈系统的可控性与可观测性
5.1.2 单变量系统的极点配置
5.1.3 多变量系统的极点配置
5.1.4 系统的可镇定问题
5.1.5 状态反馈的特征结构配置
5.2 输出反馈的极点配置
5.2.1 输出反馈系统的可控性与可观测性
5.2.2 常值输出反馈配置极点的基本定理
5.2.3 常值输出反馈配置极点的算法
5.3 动态输出反馈补偿器
5.4 解耦控制问题
5.4.1 解耦控制问题的提法
5.4.2 系统状态反馈解耦的充要条件
5.4.3 状态反馈解耦的极点配置
5.4.4 稳态解耦问题
……
参考文献2100433B
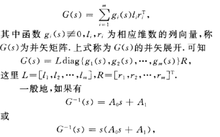
并矢矩阵概述
并矢矩阵(dyadic matrix)非奇异多项式矩阵的一种特殊表示形式.当
其中A。和A,为实常数矩阵,A。非奇异,则GCs)为并矢矩阵.如果被控制对象的传递函数矩阵是并矢矩阵,则可用并矢展开方法为它设计控制系统.
1、线性无卷积混外,本文将文献5的方法推广到卷积混合信号的分合模型中传递函数矩阵(又称为混合矩阵)为常数矩离,最后给出了语言信号分离的数值模拟结果
2、xm(k)]T(1)公式(3)中A是mxn满秩矩阵,称为混合矩阵.ICA主要用于盲源信号分离:在混合矩阵和源信号(独立成分)未知的情况下,仅利用观测信号x,尽可能真实地分离出源信号s,这就是所谓的盲源分离问题(BlindSourceSeparation,简称BSS)
3、A是m×n维的列满秩矩阵(通常A称为混合矩阵).现有研究多数假定源信号的个数已知,且观测信号向量与源信号向量具有相同的维数,即m=n
4、在这里A是M×N维未知矩阵,称为混合矩阵.向量X则是源信号的线性混合.盲源分离就是要找到分离矩阵W,使得U(t)=WX(t),W=A-1,U(t)=S(t)
5、A称为混合矩阵.盲源信号分离问题就是要从观测矢量中恢复出源信号矢量,即要找到一个分离矩阵W,通过y=Wx产生源信号的估计
6、A称为混合矩阵.图1中W是一个解混矩阵,观测信号x通过该系统后得到近似于s的输出y.该过程可由下式表示:y=Wx(2)衡量一组信号是否接近互相独立,有多种准则,即优化判据
7、A是未知的满秩矩阵,称为混合矩阵,n假设为高斯白噪声. 式(1)可以有如下变换:x=As n=Σni=1aiαiαisi n=A′s′ 文献来源
8、m×n维矩阵A称为混合矩阵.盲源分离的实质是在源信号s(t)和混合矩阵A均未知的情况下,根据观测向量x(t)找到一个分离矩阵W,使y(t)=Wx(t)成为s(t)的拷贝或估计
9、N)的线性混合,写成矩阵形式即:X(t)=AS(t)(1) 其中,A∈RN×N称为混合矩阵,它反映了介质或信道的传输特性
10、xm(k)]T为m维观测数据向量,其元素是各个传感器得到的输出,观测信号可用下面的方程描述:x(k)=As(k)(1)其中,m×n维矩阵A称为混合矩阵,其元素表示信号的混合情况 11、A称为混合矩阵,它是未知的m行n列的满秩矩阵.如果独立分量si具有单位方差,即E{sisi}=1(i=1,2,.n),则除了它的符号以外,可被唯一确定
- 相关百科
- 相关知识
- 相关专栏
- ISGB型便拆立式管道离心泵
- 废水提升泵
- 麻驾高速公路
- 拼花地板
- 水泵学
- 双联切换过滤器
- 屯溪老大桥
- 燃气轮机
- CASIO fx-9860G SD矩阵串列编程计算器实用测量程序
- 耐磨蝶阀
- 线性责任矩阵
- 瓷木地板
- 潜水泵
- UPVC电动球阀
- 碳化硅
- 巴劳木
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 电气工程及其自动化特色专业建设探索
- 分形DGS单元结构设计及其在微带电路中的应用
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 预制砌块(砖、石)挡土墙工程砌体施工安全技术交底
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 引嫩工程扩建区土壤水盐动态与防治土壤盐碱措施
- 中华华丹雨、污水管道沟槽开挖专项施工方案教学教材
- 中国工程图学学会成立工程与制造系统集成化分会
- 中国吹制玻璃行业市场前景分析预测年度报告(目录)
- 可替代现有隔热保温材料的新型材料
- 医院病房楼工程施工装饰装修工程施工控制
- 在生活中构筑自然——河南天旺园林工程有限公司剪影
- 中国机械工程学会授予材料热处理工程师资格人员名单