如果方程要求未知量y(x)及其导数y′(x)在自变量的同一点x=x0取给定的值,即y(x0 )=y0,y′(x0)= y0′,则这种条件就称为初始条件,由方程和初始条件构成的问题就称为初值问题;
而在许多实际问题中,往往要求微分方程的解在某个给定区间a ≤ x ≤b的端点满足一定的条件,如y(a) = A , y(b) = B,则给出的在端点(边界点)的值的条件,称为边界条件,微分方程和边界条件构成数学模型就称为边值问题。
边界条件造价信息
边值问题中的边界条件的形式多种多样,在端点处大体上可以写成这样的形式,Ay By'=C,若B=0,A≠0,则称为第一类边界条件或狄里克莱(Dirichlet)条件;B≠0,A=0,称为第二类边界条件或诺依曼(Neumann)条件;A≠0,B≠0,则称为第三类边界条件或洛平(Robin)条件。
总体来说,
第一类边界条件:
给出未知函数在边界上的数值;
第二类边界条件:
给出未知函数在边界外法线的方向导数;
第三类边界条件:
给出未知函数在边界上的函数值和外法线的方向导数的线性组合。
对应于comsol,只有两种边界条件:
Dirichlet boundary(第一类边界条件)—在端点,待求变量的值被指定。
Neumann boundary(第二类边界条件)—待求变量边界外法线的方向导数被指定。
再补充点初始条件:
初始条件,是指过程发生的初始状态,也就是未知函数及其对时间的各阶偏导数在初始时刻t=0的值.在有限元中,好多初始条件要预先给定的。不同的场方程对应不同的初始条件。
总之,为了确定泛定方程的解,就必须提供足够的初始条件和边界条件!
诺伊曼边界条件
在数学中,诺伊曼边界条件(Neumann boundary condition) 也被称为常微分方程或偏微分方程的“第二类边界条件”。诺伊曼边界条件指定了微分方程的解在边界处的微分。
在常微分方程情况下,如
在区间[0,1],诺伊曼边界条件有如下形式:
y'(0) = α1y'(1) = α2其中α1和α2是给定的数值。
一个区域上的偏微分方程,如
Δyy= 0(Δ表示拉普拉斯算子,诺伊曼边界条件有如下的形式
这里,ν表示边界处(向外的)法向;f是给定的函数。法向定义为
其中∇是梯度,圆点表示内积。
(1)正确确定周边炮眼的位置、
方向、深度、角度,并选用低密度、低爆速和高体积威力的炸药,是保证光面爆破成功和增强爆破效果的关键。
(2)采用预留边坡保护层、分集或分条分层布置药包、松动或抛坍洞室控制爆破进行路堑主体方量开挖,然后至坡顶向下用挖掘机配合浅眼爆破进行刷坡和清方,能适用于各种复杂地形条件的深挖石方路堑开挖,且成本低廉。
(3)采用预裂---洞室控制爆破相结合的方法进行深路堑石方深孔爆破或松动爆破方快速开挖,然后用挖掘机、推土机、装载机配合自卸气车联合清方,效果更为显著。
(4)利用有利地形进行定向爆破、抛坍(掷)业,对具有一定岩石厚度边坡路堑具有显著效果。
边界条件简介常见问题
-
假定粱在XY平面内,粱沿X方向放置,左边固定饺支座,右边滑动饺支座,那么边界为:左边(u1=0,u2=0),右边(u2=0),如果是平面粱,还应限制整根粱Z向位移,以及粱绕X轴的转动。
边界条件简介文献

 钢管玻璃润滑热挤压工艺的边界条件
钢管玻璃润滑热挤压工艺的边界条件
以P91钢为例进行了小口径钢管玻璃润滑热挤压工艺试验,记录不同挤压温度、挤压速度下的挤压力变化。以物理试验的观察结果为依据,借助于有限元软件DEFORM 2D进行模拟分析,根据稳定挤压阶段的挤压力大小,得出相应的摩擦系数,根据挤压力曲线的后期变化趋势,得出相应的换热系数。并最终得出玻璃润滑边界的换热系数q≤1.0×103J/(m2.s.℃),库仑摩擦系数μ=0.02~0.03,从而为钢管玻璃润滑热挤压工艺提供合理准确的边界参数。

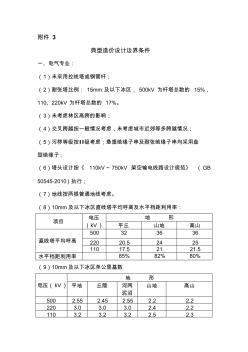 典型造价设计边界条件(V1.0版)
典型造价设计边界条件(V1.0版)
附件 3 典型造价设计边界条件 一、电气专业: (1)未采用拉线塔或钢管杆; (2)耐张塔比例: 15mm 及以下冰区, 500kV 为杆塔总数的 15%, 110、220kV 为杆塔总数的 17%。 (3)未考虑林区高跨的影响; (4)交叉跨越按一般情况考虑,未考虑城市近郊等多跨越情况; (5)污秽等级按Ⅱ级考虑;悬垂绝缘子串及耐张绝缘子串均采用盘 型绝缘子; (6)塔头设计按《 110kV~ 750kV 架空输电线路设计规范》 (GB 50545-2010)执行; (7)地线按两根普通地线考虑。 (8)10mm及以下冰区直线塔平均呼高及水平档距利用率: 项目 电压 (kV) 地 形 平丘 山地 高山 直线塔平均呼高 500 32 36 36 220 20.5 24 25 110 17.5 21 21.5 水平档距利用率 85% 82% 80% (9)10mm及以下冰区单公里
应力状态应力边界条件
应力边界条件即弹性体在外力作用下处于平衡状态的条件,是物体内部的各点的应力分量应满足平衡方程式,物体边界上各点也必须是平衡的。
由后者将导出应力边界条件。换言之,所谓应力边界条件就是在给定面力的边界上应力分量与面力分量之间的关系。
应力状态混合边界条件
混合边界条件有两种情况,一种情况是在物体的整个边界s上,一部分为已知应力,即给定应力的边界s ;另一种情况是在同一部分边界上已知部分位移和部分应力,即给定位移与应力混合边界条件。
模拟大型振动结构中波的传播是一项极具挑战性的任务,工程师必须在减小计算域尺寸与减少表面边界的反射之间做出平衡。利用 COMSOL Multiphysics® 软件的低反射边界条件,我们可以轻松将计算域减小到合理大小,同时保证仿真结果的精确度。今天,我们以岩层中的爆炸波传播建模为例,演示低反射边界条件的具体应用。
研究岩层中的爆炸波传播
隧道是十分常见的交通设施,为公路、铁路、航运,甚至是步行,都提供了更为便捷的通行方式。在地下通道施工中,为便于开挖,爆破技术常常被用于破碎岩石。

世界上最长的公路隧道——瑞士洛尔达(Lærdal)隧道利用爆破而建成。图片由 Svein-Magne Tunli 提供。在 CC BY-SA 3.0 许可下使用,通过维基共享资源分享。
在岩石爆破过程中,钻孔处会承受载荷。了解爆破时波在隧道结构中的传播过程是保证爆破操作安全可靠的关键。
对振动的大型结构中波的传播进行模拟,通常都有难度,因为我们不仅需要处理相当大的计算域,还要避免来自表面边界的反射影响结果的准确性。COMSOL Multiphysics 提供了一个简单的对策:使用低反射边界条件来截断计算域。
为了方便您清楚地了解低反射边界条件的具体应用,我们看一看“案例库”中的示例。
使用低反射边界条件模拟波的传播
低反射边界条件默认采用了相邻域的材料数据,从而创建对压力波和剪切波的完美阻抗匹配。这种方法最适用于波方向接近于壁法向的情况。
示例使用了长方体模型几何。模型的四个侧壁中有两个是对称平面。另外两个侧面的作用是截断计算域,在该切面上,岩石的深度尺寸远大于切向尺寸。长方体的尺寸及材料参数采用了模型文档中参考文献 1 提供的数据。
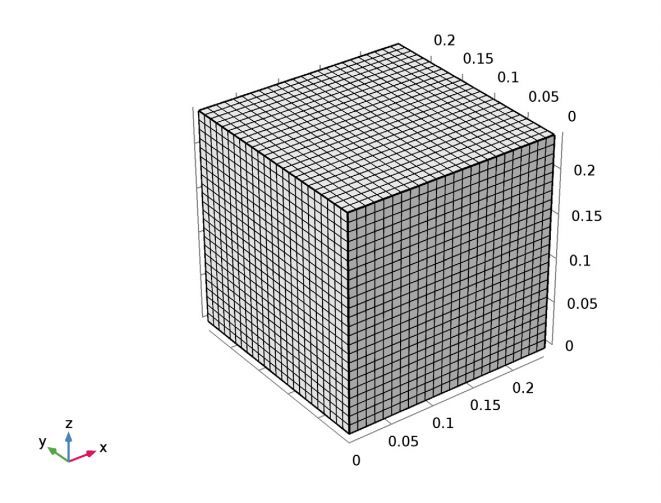
模型几何和网格。请注意,图中所示的两个侧壁是对称平面。爆破发生在两个平面与底面相交的位置。
下表显示了所使用的弹性材料的属性。请注意,这些值对应花岗岩的属性值。
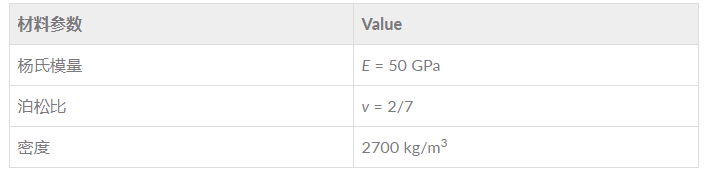
岩石的上表面为自由表面,在底面上施加了载荷,此例中为有一定持续时间的压力脉冲。载荷表示岩石内部靠近表面的地方发生了爆炸。

载荷函数。
针对长方体中波传播的瞬态研究,我们设置了 150 ms 的时间间隔。下方的仿真绘图展示了波的典型传播模式。
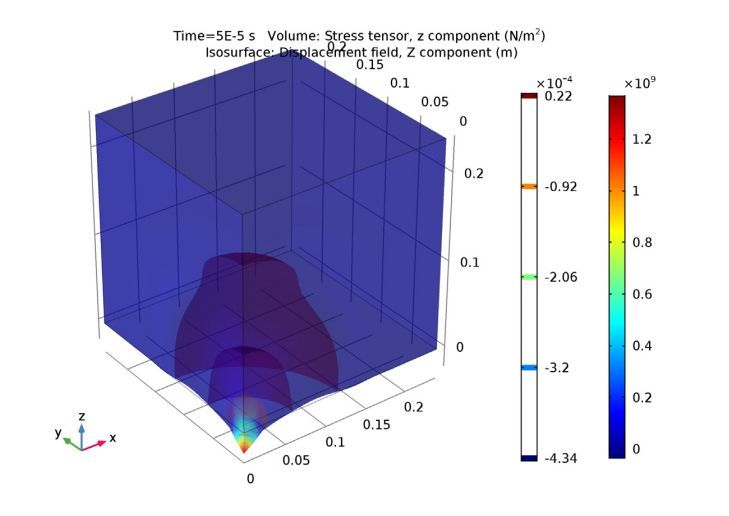
弹性波开始传播时长方体中的应力。
接着,我们对应用(蓝色实线)和未应用(绿色虚线)低反射边界条件时,岩石上表面的垂直位移进行了比较。值得注意的是,下图中的第一条和第二条垂直虚线分别表示入射和反射压力波到达表面时的解析解。两项结果均与仿真结果非常吻合。此外,如图所示,两个响应在到达预计时间后开始彼此偏离,这正是反射波造成的结果。
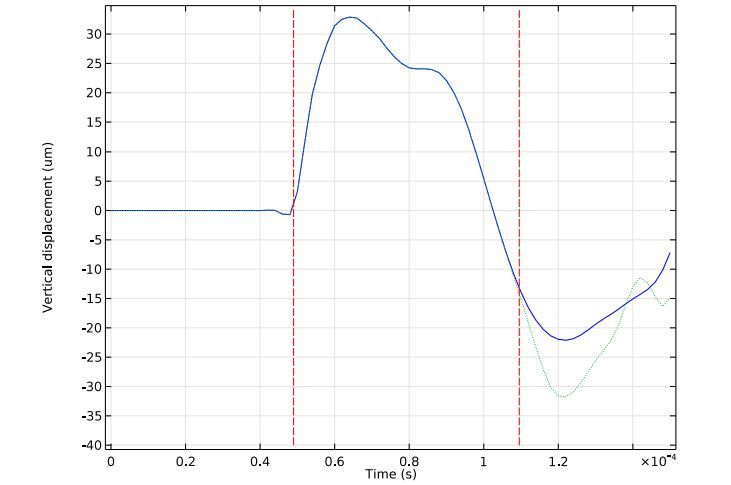
在使用和不使用低反射边界条件的情况下,比较岩石上表面的垂直位移。
本文介绍的内容只是使用低反射边界条件简化建模过程的一个案例。您可以参考此教学模型对其他仿真研究进行优化。
来源:COMSOL 中国
声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本网站观点或证实其内容的真实性;如其他媒体、网站或个人从本网站转载使用,须保留本网站注明的“来源”,并自负版权等法律责任;作者如果不希望被转载或者联系转载稿费等事宜,请与我们接洽。
对不同的边界情况,边界条件有所不同:
①固定边沿边缘各点的挠度和斜度均为零。在直角坐标系中,若x=a为固定边,则
②简支边(注:此处空格)沿简支边各点的挠度和弯矩M均为零。若x=a为简支边,则
③自由边(注:此处空格)沿自由边各点的弯矩和剪力V为零。若x=a为自由边,则
④自由角点(注:此处空格)若x=a,y=b是一个自由角点,则角点的反力R为零,即
- 相关百科
- 相关知识
- 相关专栏
- 边界检查
- 边界网关协议
- 边看边学SIEMENS数控车床加工50例(1例1视频)
- 边缘融合器
- 边角料
- 辽东学院装备与材料学院
- 辽中县土地局
- 辽宁一东电电力科技股份有限公司
- 辽宁三益家具制造有限公司
- 辽宁世纪金牛管业有限公司
- 辽宁东大东热电器有限公司
- 辽宁东戴河新区友邦信息咨询有限公司
- 辽宁东戴河新区当代置业有限公司
- 辽宁东方华升建设集团有限公司
- 辽宁东星节能新材有限公司
- 辽宁东正工程造价咨询事务所有限公司
- 永磁同步电机简介
- 以色列ELI自清洗网式过滤器和浅层介质过滤器简介
- 有关水利水电勘测设计技术标准体系情况的简介
- 工程技术分析论文地辐射采暖系统简介及常见问题
- 工程定额及造价资料电子查阅与简易预结算编制系统简介
- 广(州)深(圳)准高速铁路石龙—常坪段路基施工简介
- 基于GIS技术安徽省主要防洪工程信息系统简介
- 广东省东江—深圳供水改造工程施工图设计监理工作简介
- 乐星产电乐星产电(无锡)有限公司二期工程项目简介
- 国家玻璃质量监督检验中心安全玻璃CCC认证业务简介
- 建筑工程门窗系列产品节点图及简介PPT
- 混凝土搅拌车底盘简介
- 模具钢材料简介
- 205国道衢州段开展公路养护工程标准化工地建设活动简介
- 公路工程造价的计价与控制计价规范简介模拟试题
- 中国安全生产科学研究院注册安全工程师注册管理中心简介