
柱体、锥体、台体、球体的表面积与体积
1 cb a o o' 柱体、锥体、台体、球体的表面积与体积 教学目标:会求柱体、锥体、台体、球体的表面积和体积。 自学探究(一) 一:阅读教材第23~27页,完成下列任务 1.思考填出下列表格: 几 何 体 图形 侧面展开图表面积公式符号意义 圆 柱 r l o' o 底面积:错误!未找 到引用源。= 侧面积:错误!未找 到引用源。= 表面积:错误!未找 到引用源。= 体积:v= 错误!未找 到引用 源。: 错误!未找 到引用 源。: h: 圆 锥 l ro s 底面积:错误!未找 到引用源。= 侧面积:错误!未找 到引用源。= 表面积:错误!未找 到引用源。= 体积:v= 错误!未找 到引用 源。: 错误!

1.3.1柱体、锥体、台体的表面积与体积
1.3.1柱体、锥体、台体的表面积与体积 一、教学目标 1、知识与技能 (1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积和体积的求法。 (2)能运用公式求解,柱体、锥体和台全的全积,并且熟悉台体与术体和锥体之间 的转换关系。 (3)培养学生空间想象能力和思维能力。 2、过程与方法 (1)让学生经历几何全的侧面展一过程,感知几何体的形状。 (2)让学生通对照比较,理顺柱体、锥体、台体三间的面积和体积的关系。 3、情感与价值 通过学习,使学生感受到几何体面积和体积的求解过程,对自己空间思维能力影响。 从而增强学习的积极性。 二、教学重点、难点 重点:柱体、锥体、台体的表面积和体积计算 难点:台体体积公式的推导 三、学法与教学用具 1、学法:学生通过阅读教材,自主学习、思考、交流、讨论和概括,通过剖析实物 几何体感受几何体的特征,从而更好地完成本节课的教学目标。 2、教学用具:实
编辑推荐下载

1.3.1柱体,锥体,台体的表面积
河北武邑中学课堂教学设计 备课人授课时间 课题柱体、锥体、台体的表面积 教 学 目 标 知识与技能 柱体、锥体、台体的表面积的推导与计算,能利用公式求柱 体、锥体和台体的表面积 过程与方法启发引导,充分发挥学生的主体作用 情感态度价值观让学生体验空间几何体的表面积的求解过程与方法 重点柱体、锥体、台体的表面积的推导与计算。 难点台体的表面积公式的推导。 教 学 设 计 教学内容教学环节与活动设计 1、创设情境 (1)提出问题:在过去的学习中,我们已经学习了 正方体和长方体的表面积的求法和它们的展开图,请大 家回忆一下,它们的展开图是什么呢?怎样来求它们的 表面积? (2)设置疑问:正方体和长方体的表面积可以利用 它们的展开图(平面图形)来求面积,那么,柱体,锥 体,台体是否也可以利用它们的展开图来求呢?它们的 侧面展开图又是什么呢?如何计算它们的表面积?要是 让我们来

《1.3.1柱体、椎体、台体的表面积与体积(1)》教学案
《1.3柱体、椎体、台体的表面积与体积(1)》教学案 教 学 目 标 1.知识与技能 (1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积和体积的求法. (2)能运用公式求解,柱体、锥体和台全的全积,并且熟悉台体与术体和锥体之间的转换关系. (3)培养学生空间想象能力和思维能力. 2.过程与方法 (1)让学生经历几何全的侧面展一过程,感知几何体的形状. (2)让学生通对照比较,理顺柱体、锥体、台体三间的面积和体积的关系. 3.情感、态度与价值观 通过学习,使学生感受到几何体面积和体积的求解过程,对自己空间思维能力影响.从而增 强学习的积极性. 教学重点柱体、锥体、台体的表面积和体积计算 教学难点台体体积公式的推导 教学方法学生通过阅读教材,自主学习、思考、交流、讨论和概括,通过剖析实物几何体感 受几何体的特征,从而更好地完成本节课的教学
柱体、锥体、台体的表面积和体积课件热门文档

《1.3.1柱体、椎体、台体的表面积与体积》教学案3
《1.3.1柱体、椎体、台体的表面积与体积》教学案3 一、教学目标 1、知识与技能 (1)通过对柱、锥、台体的研究,掌握柱、锥、台的表面积和体积的求法. (2)能运用公式求解,柱体、锥体和台全的全积,并且熟悉台体与术体和锥体之间的转 换关系. (3)培养学生空间想象能力和思维能力. 2、过程与方法 (1)让学生经历几何全的侧面展一过程,感知几何体的形状. (2)让学生通对照比较,理顺柱体、锥体、台体三间的面积和体积的关系. 3、情感与价值 通过学习,使学生感受到几何体面积和体积的求解过程,对自己空间思维能力影响.从 而增强学习的积极性. 二、教学重点、难点 重点:柱体、锥体、台体的表面积和体积计算 难点:台体体积公式的推导 三、学法与教学用具 1、学法:学生通过阅读教材,自主学习、思考、交流、讨论和概括,通过剖析实物几 何体感受几何体的特征,从而更好

空间几何体的表面积和体积球、柱、锥、台的表面积和体积的计算公式及其应用
空间几何体的表面积和体积 球、柱、锥、台的表面积和体积的计算公式及其应用 二.课标要求: 了解球、棱柱、棱锥、台的表面积和体积的计算公式。 三.命题走向 近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已 知面积或体积求某些元素的量或元素间的位置关系问题。即使考查空间线面的 位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、 性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问 题转化为基本几何体的求积问题,会用体积转化求解问题,会把立体问题转化为 平面问题求解,会运用“割补法”等求解。 由于本讲公式多反映在考题上,预测2008年高考有以下特色: (1)用选择、填空题考查本章的基本性质和求积公式; (2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多 面体和旋转体中某些元素有关的计算问题; [教
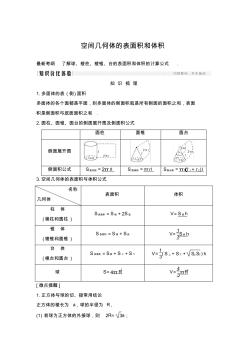
空间几何体的表面积和体积
空间几何体的表面积和体积 最新考纲了解球、棱柱、棱锥、台的表面积和体积的计算公式. 知识梳理 1.多面体的表(侧)面积 多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面 积是侧面积与底面面积之和. 2.圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱圆锥圆台 侧面展开图 侧面积公式s圆柱侧=2πrls圆锥侧=πrls圆台侧=π(r1+r2)l 3.空间几何体的表面积与体积公式 名称 几何体 表面积体积 柱体 (棱柱和圆柱) s表面积=s侧+2s底v=s底h 锥体 (棱锥和圆锥) s表面积=s侧+s底v= 1 3s底h 台体 (棱台和圆台) s表面积=s侧+s上+s下v= 1 3(s上+s下+s上s下)h 球s=4πr 2v= 4 3πr 3 [微点提醒] 1.正方体与球的切、

圆柱体积表面积和体积比较练习课PPT课件
圆柱体积表面积和体积比较练习课PPT课件
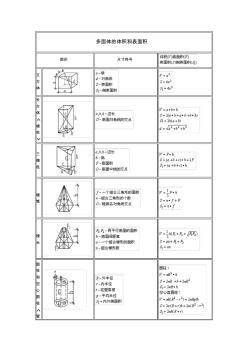
多面体的体积和表面积计算公式大全
多面体的体积和表面积 图形尺寸符号 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 棱 锥 棱 台 圆 柱 和 空 心 圆 柱 ∧ 管 ∨ 斜 线 直 圆 柱 直 圆 锥 圆 台 球 球 扇 形 ∧ 球 楔 ∨ 球 缺 圆 环 体 ∧ 胎 ∨ 球 带 体 桶 形 椭 球 体 a,b,c-半轴 交 叉 圆 柱 体 梯 形 体 常用图形求面积公式 图形尺寸符号面积(f)表面积(s) 正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形 正 多 边 形 菱 形 梯 形 圆 形 椭 圆 形 a·b-主轴f=(π/4)a·b 扇 形 弓 形 圆 环 部 分 圆 环 新 月 形 ld/102d/103d/104d/105d/106d/107d/10 p0.400.791.181.561.912.252.55 抛 物 线 形
柱体、锥体、台体的表面积和体积课件精华文档
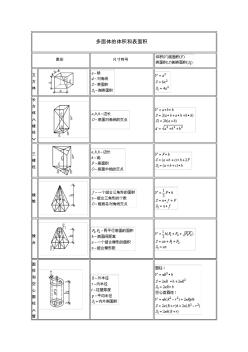
施工员计算公式大全(多面体的体积和表面积)
多面体的体积和表面积 图形尺寸符号 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 棱 锥 棱 台 圆 柱 和 空 心 圆 柱 ∧ 管 ∨ 斜 线 直 圆 柱 直 圆 锥 圆 台 球 球 扇 形 ∧ 球 楔 ∨ 球 缺 圆 环 体 ∧ 胎 ∨ 球 带 体 桶 形 椭 球 体 a,b,c-半轴 交 叉 圆 柱 体 梯 形 体 常用图形求面积公式 图形尺寸符号面积(f)表面积(s) 正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形 正 多 边 形 菱 形 梯 形 圆 形 椭 圆 形 a·b-主轴f=(π/4)a·b 扇 形 弓 形 圆 环 部 分 圆 环 新 月 形 ld/102d/103d/104d/105d/106d/107d/10 p0.400.791.181.561.912.252.55 抛 物 线 形
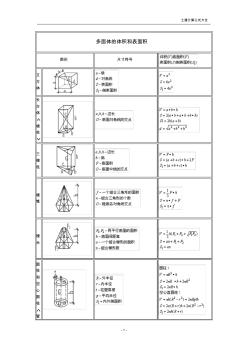
土建计算公式大全(多面体体积和表面积)1
土建计算公式大全 -1- 多面体的体积和表面积 图形尺寸符号 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 棱 锥 棱 台 圆 柱 和 空 心 圆 柱 ∧ 管 土建计算公式大全 -2- ∨ 斜 线 直 圆 柱 直 圆 锥 圆 台 球 球 扇 形 ∧ 球 楔 ∨ 土建计算公式大全 -3- 球 缺 圆 环 体 ∧ 胎 ∨ 球 带 体 桶 形 椭 球 体 a,b,c-半轴 交 叉 圆 柱 体 土建计算公式大全 -4- 梯 形 体 常用图形求面积公式 图形尺寸符号面积(f)表面积(s) 正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形 正 多 边 形 土建计算公式大全 -5- 菱 形 梯 形 圆 形 椭 圆 形 a·b-主轴f=(π/4)a·b 扇 形 弓 形 圆 环 土建计算公式大全 -6- 部 分 圆

桥台锥体填土及护坡体积积分法
**资讯http://www.***.*** **资讯http://www.***.***
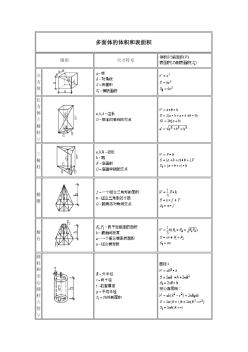
实用多面体的体积和表面积计算方式-面积计算公式大全
实用多面体的体积和表面积计算方式-面积计算公式大全

桥台锥体极座标放样
?1994-2010chinaacademicjournalelectronicpublishinghouse.allrightsreserved.http://www.cnki.net ?1994-2010chinaacademicjournalelectronicpublishinghouse.allrightsreserved.http://www.cnki.net ?1994-2010chinaacademicjournalelectronicpublishinghouse.allrightsreserved.http://www.cnki.net ?1994-2010chinaacademicjournalelectronicpublishinghouse.allrightsr
柱体、锥体、台体的表面积和体积课件最新文档
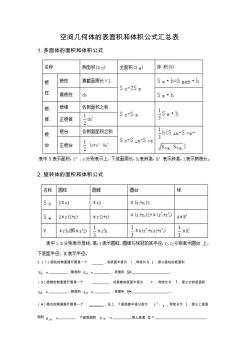
空间几何体的表面积和体积公式汇总表
空间几何体的表面积和体积公式汇总表 1.多面体的面积和体积公式 2.旋转体的面积和体积公式 3.(1)圆柱的侧面展开图是一个,设底面半径为r,母线长为l,那么圆柱的底面积 底s,侧面积侧s,表面积s=。 (3)圆锥的侧面展开图是一个,设圆锥的底面半径为r,母线长为l,那么它的底面积 底s,侧面积侧s,表面积s=。 (4)圆台的侧面展开图是一个,设上、下底面圆半径分别为r、r,母线长为l,那么上底面 面积 上底s,下底面面积下底s那么表面s。 4、正四面体的结论:设正四面体的棱长为a,则这个正四面体的 (1)全面积:s全=32a;(2)体积:v=32 12 a;(3)对棱中点连线段的长:d= 2 2 a; (4)对棱互相垂直。(5)外接球半径:r= 6 4a;(6)

计算表面积和体积练习题
-1- 表面积练习题 1、做10个棱长8厘米的正方体铁框架,至少需多长的铁丝? 2、用铁皮做一个铁盒,使它的长、宽、高分别是1.8分米,1.5分米和1.2分米,做一个这 样的铁盒至少要用铁皮多少平方米? 3、做一个没盖的正方体玻璃鱼缸,棱长是3分米,至少需要玻璃多少平方米? 4、我们学校要粉刷教室,教室长8米,宽7米,高3.5米,扣除门窗、黑板的面积13.8平 方米,已知每平方米需要5元涂料费。粉刷一个教室需要多少钱? 5、一个商品盒是棱长为6厘米的正方体,在这个盒的四周贴上商标,贴商标的面积最大是多 少平方厘米? 6、木版做长、宽、高分别是2.8分米,1.5分米和2.2分米抽屉,做5个这样的抽屉至少要 用木版多少平方米? 7.有一个养鱼池长18米,宽12米,深3.5米,要在养鱼池各个面上抹一层水泥,防止渗

71582_多面体的体积和表面积计算公式大全
多面体的体积和表面积 图形尺寸符号 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 棱 锥 棱 台 圆 柱 和 空 心 圆 柱 ∧ 管 ∨ 斜 线 直 圆 柱 直 圆 锥 圆 台 球 球 扇 形 ∧ 球 楔 ∨ 球 缺 圆 环 体 ∧ 胎 ∨ 球 带 体 桶 形 椭 球 体 a,b,c-半轴 交 叉 圆 柱 体 梯 形 体 常用图形求面积公式 图形尺寸符号面积(f)表面积(s) 正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形 正 多 边 形 菱 形 梯 形 圆 形 椭 圆 形 a·b-主轴f=(π/4)a·b 扇 形 弓 形 圆 环 部 分 圆 环 新 月 形 ld/102d/103d/104d/105d/106d/107d/10 p0.400.791.181.561.912.252.55 抛 物 线 形
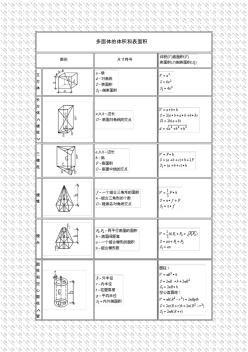
施工员常用多面体的体积和表面积计算公式大全
多面体的体积和表面积 图形尺寸符号 立 方 体 长 方 体 ∧ 棱 柱 ∨ 三 棱 柱 棱 锥 棱 台 圆 柱 和 空 心 圆 柱 ∧ 管 ∨ 斜 线 直 圆 柱 直 圆 锥 圆 台 球 球 扇 形 ∧ 球 楔 ∨ 球 缺 圆 环 体 ∧ 胎 ∨ 球 带 体 桶 形 椭 球 体 a,b,c-半轴 交 叉 圆 柱 体 梯 形 体 常用图形求面积公式 图形尺寸符号面积(f)表面积(s) 正 方 形 长 方 形 三 角 形 平 行 四 边 形 任 意 四 边 形 正 多 边 形 菱 形 梯 形 圆 形 椭 圆 形 a·b-主轴f=(π/4)a·b 扇 形 弓 形 圆 环 部 分 圆 环 新 月 形 ld/102d/103d/104d/105d/106d/107d/10 p0.400.791.181.561.912.252.55 抛 物 线 形

圆柱的表面积PPT课件
圆柱的表面积PPT课件
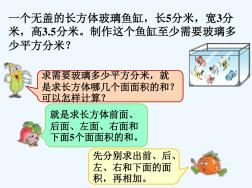
玻璃鱼缸_长方体、正方体的表面积
玻璃鱼缸_长方体、正方体的表面积
阀体阀座锥体研磨装置的设计与实施
我厂成功开发了应用于化纤行业的鼓风机,该设备中的安全回流装置是控制系统压力均衡的重要部分。其关键零件阀体、阀座的锥度配合面需进行研磨,才能够保证锥面的配合精度,达到设计的气密性要求。因阀体、阀座材质为不锈钢且体积较大,手工研磨锥面时既费时又费力。阀体、阀座结构简图如图1所示。
椭球体封头设计施工三阶计算(下料直径,表面积,容积)
椭球体封头设计施工三阶计算(下料直径,表面积,容积)
椭球体封头设计施工三阶计算(下料直径,表面积,容积)
椭球体封头设计施工三阶计算(下料直径,表面积,容积)
基于光谱特征的长江口细颗粒泥沙絮凝体投影表面积和沉速分析
2009年5月23日—6月2日在长江口南槽九段沙水域,利用便携式地物光谱仪和现场激光粒度仪分别测量了水体光谱反射率和细颗粒泥沙絮凝体现场特性以研究两者之间的关系,测量时同步采集了水样测量悬沙浓度(ssc)。研究显示:①水体光谱反射率随絮凝体投影表面积(psa)的增加而增大,光谱曲线在350~950nm波段间存在两个明显反射峰,分别以690~720nm和810nm波长为中心;②絮凝过程改变细颗粒泥沙的水体反射光谱特征,导致ssc与光谱反射率的相关性低于psa与光谱反射率的相关性。psa与波长>715nm波段光谱反射率的相关性r>0.7,p<0.01;③可选择常用卫星遥感可见光、近红外通道范围,且psa与光谱反射率相关性较高的波段,建立psa与单波段光谱反射率和多波段光谱反射率组合比值的拟合关系式,其中单波段860nm(r=0.9227,p<0.001)和860/670多波段组合(r=0.9373,p<0.001)的指数方程预测效果均最优;④构建了光谱反射率与絮凝体沉速间的幂函数拟合关系式(r=0.8337,p<0.001),为监测长江口大尺度区域絮凝体psa和ws的空间分布和动态变化提供了一种新的方法。
柱体、锥体、台体的表面积和体积课件相关
文辑推荐
知识推荐
百科推荐

职位:建筑物安全检定员
擅长专业:土建 安装 装饰 市政 园林


