优化的 GM(1,1)模型在建筑业总产值预测中的应用
将正弦函数变换和 Lagrange 插值法相结合,对 GM(1,1)模型的原始数据和背景值同时进行优化,使用优化的 GM(1,1)模型对2003年-2012年建筑业总产值进行了实证研究,研究结果说明了该优化模型具有高精度性,拓广了 GM(1,1)的使用范围。

多元线性回归模型在江苏建筑业总产值预测中的效果分析
建筑业是国民经济的支柱产业,是重要的物质生产部门。文章基于江苏2000-2016年建筑业经济指标的时间序列数据,以江苏建筑业的流动资产、薪酬、用电量作为解释变量,用建筑业总产值作为被解释变量,通过建立多元回归模型进行实证分析,发现流动资产、薪酬、用电量总产值具有较强的显著性,江苏建筑业总产值的实际值与预测值的误差均值百分比(mpe)和误差绝对百分比(mape)分别为0.08%、5.34%,说明模型具有良好的预测效果。
编辑推荐下载
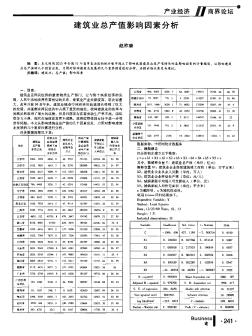
建筑业总产值影响因素分析
本文利用2013年全国31个省市自治区的统计数字建立了影响我国建筑业总产值增长的各影响因素的计量模型。从影响建筑业总产值的几个因素出发,力图对影响建筑业发展的几个重要因素进行分析,并提出相关意见与建议。
中国建筑业总产值的多元线性回归分析
在建筑业的企业类型视角下,从国有企业、集体企业、港澳台商投资企业、外商投资企业、其他等5个方面建立建筑业总产值影响因素多元线性回归模型,用2013年中国统计年鉴中2000—2012年建筑业总产值的数据对构建的线性回归模型加以可行性验证,结果显示建筑业总产值与参与建筑业的企业类型存在显著的多元线性回归关系。
优化的GM1模型建筑业总产值预测中的应用热门文档

我国建筑业总产值影响因素分析
改革开放以后,我国建筑业得到了快速的发展,为中国经济的持续增长做出了重要贡献.本文针对我国建筑业的发展状况,选取2002-2016年相关数据,利用e-views软件,通过建立模型和模型的检验与调整,得出模型的应用与对策措施.希望本文有助于我国建筑业总产值的持续增长.

各地区建筑业总产值对建筑业企业利润总额的影响 (2)
计量经济学 期末实验报告 实验名称:各地区建筑业总产值对建 筑业企业利润总额的影响 姓名: 学号: 班级: 指导教师: 时间: 一、研究的背景 近年来,由于房地产事业的快速发展,同时也带动了建筑业的总产值业的飞速增长, 为了研究各地区建筑业总产值和建筑业企业利润总额之间的关系,预测未来的增长趋势, 需建立计量经济学模型。 二、指标选取和数据搜集 从《中国统计年鉴》可以收集到以下数据: 表1.各地区建筑业总产值和建筑业企业利润总额(单位:万元) 地区建筑业企业利润总额(y)建筑业总产值(x) 北京960256.425767692 天津379211.612219419 河北446520.816146909 山西194565.910607041 内蒙古353362.66811038.3 辽宁836846.621000402 福建375

各地区建筑业总产值对建筑业企业利润总额的影响
计量经济学 期末实验报告 实验名称:各地区建筑业总产值对建 筑业企业利润总额的影响 姓名: 学号: 班级: 指导教师: 时间: 一、研究的背景 近年来,由于房地产事业的快速发展,同时也带动了建筑业的总产值业的飞速增长, 为了研究各地区建筑业总产值和建筑业企业利润总额之间的关系,预测未来的增长趋势, 需建立计量经济学模型。 二、指标选取和数据搜集 从《中国统计年鉴》可以收集到以下数据: 表1.各地区建筑业总产值和建筑业企业利润总额(单位:万元) 地区建筑业企业利润总额(y)建筑业总产值(x) 北京960256.425767692 天津379211.612219419 河北446520.816146909 山西194565.910607041 内蒙古353362.66811038.3 辽宁836846.621000402 福建375

浅谈房屋建筑施工企业建筑业总产值的统计核算
建筑业总产值是指以货币表现的建筑业企业在一定时期内生产的建筑业产品和服务的总和,正确的统计方法要克服统计中重报、漏报、混淆概念等造成的总产值统计失真,通过进一步的分析,提出应当从认真读解报表制度、加强对原始数据的归集、整理、及时掌握工程进展、理清工程进度款与建筑业总产值的关系等方面入手,提高建筑业总产值统计的水平。

黑龙江力争2012年建筑业总产值实现增长15%
黑龙江省政府日前透露,从2009年至2012年前,这个省建筑总产值将力争达到1500亿元,建筑业对外承包产值占建筑业总产值的30%;力争建筑业总产值、增加值和利税总额年均分别增长15%、17%和15%,建筑业整体竞争能力和市场份额达到国内中等以上水平。争取3至5年时间,打造3个特级资质、20个一级资质建筑企业,
优化的GM1模型建筑业总产值预测中的应用精华文档
一季度全国建筑业总产值3.4万亿元同比增长10.8%
4月17日,国家统计局公布了今年一季度全国经济运行情况.经初步核算,1~3月,国内生产总值180683亿元,按可比价格计算,同比增长6.9%.备受业内人士关注的建筑业总产值数据也同时公布,1~3月,全国建筑业总产值34189亿元,同比增长10.8%,高于gdp增速.业内人士表示,再次跃上两位数的增速无疑给正在走出低迷慢慢回暖的中国建筑业一剂"强行针".

浅析房屋建筑施工公司建筑业总产值的统计与核算
建筑业总产值是指建筑业在一定时期内以货币形式产生的建筑业产品和服务的总和。正确的统计方法必须克服统计重述、遗漏和混淆造成的总产值疏漏、统计失真等,应认真阅读报表系统制度,加强对原始数据的收集和整理,及时掌握项目的进展情况,明确进度之间的关系该项目的总产值和建筑业的总产值,提高行业产值统计程度。
影响新疆生产建设兵团建筑业总产值的相关因素的分析
根据1996年《新疆生产建设兵团统计年鉴》有关建筑业的统计资料,利用线性回归方法,对影响兵团建筑业总产值的因素进行了分析。结果表明,主要的影响因素为:职工年平均人数、技术装备率和劳动生产率,而劳动生产率是影响总产值的最主要的影响因素,同时,要提高兵团建筑业总产值,其技术装备率也有待于提高。

GM(1,1)优化模型在基坑变形预测中的应用
gm(1,1)优化模型在基坑变形预测中的应用——基坑边坡系统是一典型的灰色系统。其变形发展过程可用灰色系统理论进行预测。本文在常规全息gm(1,1)模型的基础上,采用等维新息迭代法gm(1,1)模型对郑州太阳城紫荆花园基坑变形进行模拟预测,结果表明了迭代法g...
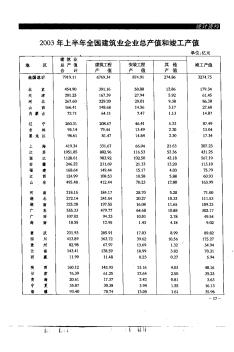
2003年上半年全国建筑业企业总产值和竣工产值
2003年上半年全国建筑业企业总产值和竣工产值 建笛1i【, 地区总产值建筑工程安装工程其他竣工产值 合计产值产值产值 全国总计7919.116769.34874.91274.863274.75 北京454.90391.1650.8812.86179.34 天津201.25167.3927.945.9261.45 河北267.6o229.2o29.019.3886.30 山西166.41148.6814.563.1727.60 内蒙古72.7164.117.471.1314.87 辽宁260.31208_6746.415.2387.49 吉林95.1479.4413.492.2013.04 黑龙江98.6181.4714.84
优化的GM1模型建筑业总产值预测中的应用最新文档
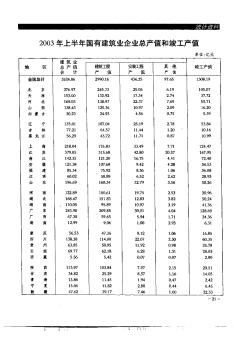
2003年上半年国有建筑业企业总产值和竣工产值
2003年上半年国有建筑业企业总产值和竣工产值 单位:亿元 毒各4智、ii, 地区总产值建筑瑰安装卫陧其他竣工产值 合计产值产值产值 全国总计3524.062990.16436.2597.651308.19 北京276.97245.7325.056.19105.07 天津153.0o132.9217.342.7437.72 河北169.03138.9722.377.6955.71 山西138.43125.3610.972.0916.20 内蒙古30.2324.934.560.755.39 辽宁135.011o7.0425.192.7853.84 吉林77.2164.5711.441.20⋯10.16 黑龙江56.2943.

GM(1,1)、GM(1,N)联合模型在建筑物沉降预测中的应用
鉴于gm(1,n)模型预测精度高及gm(1,1)所需统计数据数量少的优点,通过自相关理论,把gm(1,1)和gm(1,n)两者有机结合形成一个联合模型,以进一步提高灰色模型的预测精度。该文在沉降资料的基础上,利用该联合模型对南京一泵站的沉降进行了分析预报,其结果与回归模型和gm(1,1)模型进行了比较,最后得出了基于自相关理论的gm(1,1)、gm(1,n)联合预测模型,其精度可靠,可信度高,预报结果也与实际情况相吻合,从而证明了该方法在实际工程中的可行性。

双优化GM(1,1)新模型在路基沉降预测中的应用
路基沉降预测一直是道路工程领域的研究重点和难点。常用的gm(1,1)模型所预测的路基沉降值精度相对较低,特别当数据序列急剧变化时,gm(1,1)模型的误差值可能会更大甚至失效。针对传统gm(1,1)模型存在的问题,通过改变初始值,增加扰动因素β优化初始条件。同时利用非齐次指数函数拟合模型中变量的一次累加生成序列优化背景值,提出了初始条件和背景值双优化的新gm(1,1)模型。通过matlab软件编程实例计算表明,双优化之后的新gm(1,1)模型较原模型相比,其预测精度有了较大幅度的提高。

双优化GM(1,1)新模型在路基沉降预测中的应用
路基沉降预测一直是道路工程领域的研究重点和难点。常用的gm(1,1)模型所预测的路基沉降值精度相对较低,特别当数据序列急剧变化时,gm(1,1)模型的误差值可能会更大甚至失效。针对传统gm(1,1)模型存在的问题,通过改变初始值,增加扰动因素β优化初始条件。同时利用非齐次指数函数拟合模型中变量的一次累加生成序列优化背景值,提出了初始条件和背景值双优化的新gm(1,1)模型。通过matlab软件编程实例计算表明,双优化之后的新gm(1,1)模型较原模型相比,其预测精度有了较大幅度的提高。
LED电源总产值高 行业厂商将伺机出击
2013年,我国led驱动电源数量将达到700万台以上,市场规模将扩大到17.5亿;2016年,led照明电源供应器销售量将达到40亿个,总产值高达100亿美元。总之,led驱动电源市场前景可观。

GM(1,1)模型在凤山隧道变形预测中的应用
针对gm(1,1)模型在隧道围岩变形预测中的缺点,提出采用模型维数控制的方法进行预测.研究gm(1,1)模型的数学原理,针对隧道围岩的变形特点利用数学方法改进模型背景值的计算公式,并利用等维替代法不断更新预测模型.通过对比传统gm(1,1)模型可知,改进后的模型预测精度有较大提高,能较好预测围岩实际变形情况和趋势.

改进GM(1,1)模型在基坑变形预测中的应用
分析得出原始gm(1,1)模型对应的灰微分方程仅是白化微分方程的梯形积分形式,因此以辛普生求积公式为基础建立了新的灰微分方程,而辛普生求积公式也是一种近似表达形式,因而对新的灰微分方程添加动态扰动项,以弥补灰微分方程与白化微分方程的差别,同时对初始值添加修正项,使其更加符合最小二乘法思想。将改进后的gm(1,1)模型应用到基坑变形预测中,实例应用结果显示,改进的gm(1,1)模型具有较高的预测精度。

基于粒子群优化的分数阶PFGM(1,1)模型在建筑物沉降预测中的应用
针对传统的灰色预测模型对建筑物沉降预测精度不高、拟合数据较差的问题,在传统的gm(1,1)模型基础上提出了分数阶建模的思想,采用粒子群优化算法求解最优分数阶次,建立基于粒子群优化的分数阶pfgm(1,1)模型.实例计算表明,分数阶fgm(1,1)模型可以提高建筑物沉降的预测精度,通过粒子群优化算法选取最优阶次可以进一步提高预测精度和误差检验等级.由此可见,基于粒子群优化的分数阶pfgm(1,1)模型对建筑物的沉降控制有着重要的指导作用.

GM-LSSVM模型在建筑能耗预测中的应用
为提高大型公共建筑能耗的预测精度,提出一种基于灰色模型和最小二乘向量机方法(gm-lssvm)的办公能耗预测模型.该方法结合灰色建模计算简单的特点,以及最小二乘支持向量机非线性拟合能力和泛化能力强的优势,充分发掘样本数据的规律,并以粒子群优化算法进行模型参数选择.根据福州某大型公共建筑能耗数据,通过本研究提出的方法建立预测模型,并与神经网络模型以及最小二乘支持向量机模型的预测结果进行比较,验证了该方法具备较高的预测精度和较强的泛化能力.
改进的GM-AR组合模型在地铁沉降预测中的应用
灰色预测模型对沉降的整体趋势有很好地预测结果,时序模型针对随机性的数据进行预测,二者结合一定程度上可提高预测的精度。文中通过改进gm-ar模型并将其应用于地铁沉降预测中,同时与灰色预测模型和gm-ar组合模型的预测精度进行对比分析。结果表明,改进后gm-ar模型可以有较好的预测效果。
优化的GM1模型建筑业总产值预测中的应用相关
文辑推荐
知识推荐
百科推荐

职位:高级暖通空调工程师
擅长专业:土建 安装 装饰 市政 园林



