造价通

树冰喷头与水面的距离
云知
  • 云知
  • 资讯
  • 资料
  • 参考价
  • 信息价
  • 市场价
  • 供应商
  • 询价
注册 | 登录
更新时间：2024.11.23
头 条 17个树冰喷头 4个蒲公英喷头 怎么配水泵 4个水泵
这就要看你是如何设计喷泉类型了，主要是要将同期喷水的连接在同一个泵体上，用程控开关分别控制水泵工作时间就可以了。
相关推荐
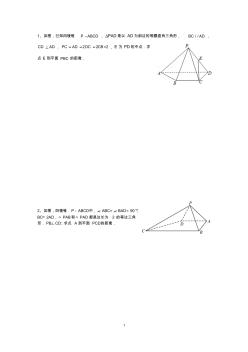
点到平面的距离(1)

点到平面的距离(1)

格式：pdf

大小：168KB

页数： 4页

1 1、如图，已知四棱锥 P ABCD ， PAD是以 AD为斜边的等腰直角三角形， / /BC AD ， CD AD ， 2 2 =2PC AD DC CB ， E 为 PD的中点．求 点 E 到平面 PBC 的距离 . 2、如图，四棱锥 P－ABCD中，∠ ABC＝∠ BAD＝ 90°， BC＝ 2AD，△ PAB和△ PAD都是边长为 2 的等边三角 形． PB⊥CD；求点 A到平面 PCD的距离． 2 3 、 如 图 ， 在 四 棱 锥 P ABCD 中 ， / /C D P A D A BCD平面 ， 4 4, ,CD AD AB AC PA且 M 是线段 CP上一点 / / 1 1 = = 4 2 PM PC AP AD P DMB A平求 面且 ， 证 ， M ABCD并求点 到平面 的距离 4、如图，四棱锥 P ABCD中，底面 ABCD 为平行四边形， 60DAB

在线阅读 立即下载
点到平面的距离(文科)

点到平面的距离(文科)

格式：pdf

大小：223KB

页数： 4页

点到平面的距离 (文科数学 ) 1．【2018 年全国卷 II 文】如图，在三棱锥 中， ， ， 为 的中点． （1）证明： 平面 ； （2）若点 在棱 上，且 ，求点 到平面 的距离． 【答案】（1）见解析（ 2） ． （2）作 CH⊥OM，垂足为 H．又由（ 1）可得 OP⊥CH，所以 CH⊥平面 POM．故 CH的长 F E D C BA 为点 C到平面 POM 的距离．由题设可知 OC= =2，CM = = ，∠ ACB=45°．所以 OM= ，CH= = ． 所以点 C到平面 POM 的距离为 ． 点睛：立体几何解答题在高考中难度低于解析几何， 属于易得分题， 第一问多以线面的证明 为主，解题的核心是能将问题转化为线线关系的证明； 本题第二问可以通过作出点到平面的 距离线段求解，也可利用等体积法解决 . 2. （2005年福建高考题）如图 1，直二面角 EABD 中，四边形 A

在线阅读 立即下载

最新知识

树冰喷头与水面的距离
点击加载更多>>
专题概述
相关话题
资料下载
相关资讯
树冰喷头与水面的距离相关专题

分类检索：

关于造价通| 开放平台| 商务合作| 帮助中心| 意见反馈| 联系我们| 网站地图| 官方微博

© 2006- WWW.ZJTCN.COM 粤ICP备08028283号 增值电信业务经营许可证：粤B2-20090350