平面问题的极坐标解法——一、用极坐标求解的平面问题 构件特征：圆筒、圆盘、扇形板．半平面体．楔形体、带孔物体。 应力分量：r (r, q), q (r, q), rq = qr(r, q) 应变分量：er , eq , g rq = g qr(r, q) 位...
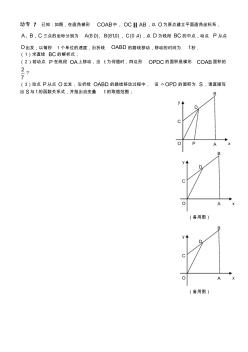
动专 7 已知：如图，在直角梯形 COAB中， OC AB∥ ，以 O为原点建立平面直角坐标系， A B C， ， 三点的坐标分别为 (8 0) (810) (0 4)A B C，， ， ， ， ，点 D为线段 BC的中点，动点 P 从点 O出发，以每秒 1个单位的速度，沿折线 OABD 的路线移动，移动的时间为 t秒． （1）求直线 BC的解析式； （2）若动点 P在线段 OA上移动，当 t为何值时，四边形 OPDC的面积是梯形 COAB面积的 2 7 ？ （3）动点 P从点 O出发，沿折线 OABD 的路线移动过程中， 设 OPD△ 的面积为 S，请直接写 出 S与 t的函数关系式，并指出自变量 t的取值范围； A B D C O P x y A B D C O x y （备用图） A B D C O x y （备用图）
热门知识
平面三轴坐标法-
话题： 工程造价mutong1004
-
话题： 工程造价greenfuture
-
话题： 工程造价xiaolei10086
精华知识
平面三轴坐标法-
话题： 地产家居gao6127377
-
话题： 路桥市政zhoushenqc
最新知识
平面三轴坐标法-
话题： 工程造价zhanglimint
-
话题： 建筑施工talentxuke
-
话题： 建筑设计lailejiuhao
相关问答
平面三轴坐标法-
话题： 工程造价zhongxiaojun
-
话题： 建筑设计szmirankeji1
-
话题： 造价软件jervis2094
平面三轴坐标法相关专题
- 楼面结构平面图
- 怎么制作平面结构图
- 结构平面图楼梯配筋
- 钢结构次梁平面图怎么看
- 房屋结构平面图立体图
- 什么是屋面结构平面图
- 储藏室顶结构平面布置图
- 平面图和结构图的阳台标注
- 钢结构观光电梯平面
- 钢结构商铺平面立面剖面
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 有源配电网设备利用率影响因子体系及其价值计算方法
- 有限元法在软土浅埋隧道施工过程的动态模拟中的应用
- 新型基于热力学法的水泵效率数学模型及应用
- 一拖一变频柜电气原理图(三晶VM1000B系列)
- 原来这就是辨别冷热水管正确方法商家终于肯说实话了
- 云南省建设工程造价协会优秀工程咨询成果奖评选办法
- 中国民宿消费市场格局分析及十三五发展环境分析报告
- 新的基于NGA/PCA和SVM的特征提取方法
- 乙烯基树脂混凝土电解槽的性能及在湿法冶金中的应用
- 应用清单招标与经评审的最低投标价法评标的几点思考
- 定征复合板材粘接层性质的非线性超声兰姆波方法
- 圆形隧道反向曲线隧道中心线两种偏移计算方法的比较
- 以信息化建设为切入点 推动“三基”工作全面落实
- 杂散电容对交流法微电容测量电路噪声特性影响的分析
- 招标师招标采购法律法规与政策题型分析辅导材料
- 主要用固体工业废渣生产硫铝酸盐水泥熟料的方法