- 首页 >
- > 空间几何体的结构习题

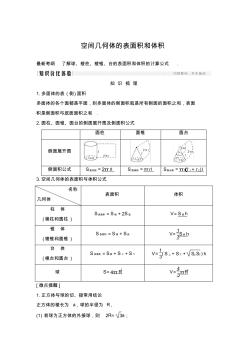
空间几何体的表面积和体积 最新考纲 了解球、棱柱、棱锥、台的表面积和体积的计算公式 . 知 识 梳 理 1.多面体的表 (侧)面积 多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面 积是侧面积与底面面积之和 . 2.圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱 圆锥 圆台 侧面展开图 侧面积公式 S圆柱侧=2π rl S 圆锥侧=π rl S圆台侧=π(r 1+ r 2) l 3.空间几何体的表面积与体积公式 名称 几何体 表面积 体积 柱 体 (棱柱和圆柱 ) S表面积=S 侧+2S 底 V=S 底h 锥 体 (棱锥和圆锥 ) S 表面积=S 侧+S底 V= 1 3S底 h 台 体 (棱台和圆台 ) S 表面积=S侧+S 上+S 下 V= 1 3( S 上+S下+ S上S下) h 球 S=4π R 2 V= 4 3πR 3 [微点提醒 ] 1.正方体与球的切、

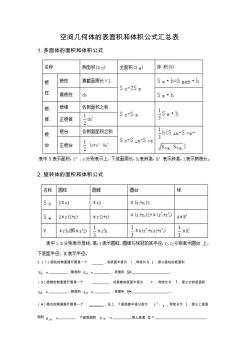
空间几何体的表面积和体积公式汇总表 1.多面体的面积和体积公式 2.旋转体的面积和体积公式 3.(1)圆柱的侧面展开图是一个 ,设底面半径为 r,母线长为 l ,那么圆柱的底面积 底S ,侧面积 侧S ,表面积 S= 。 (3)圆锥的侧面展开图是一个 ,设圆锥的底面半径为 r ,母线长为 l ,那么它的底面积 底S ,侧面积 侧S ,表面积 S= 。 (4)圆台的侧面展开图是一个 ,设上、下底面圆半径分别为 r 、 r ,母线长为 l ,那么上底面 面积 上底S ,下底面面积 下底S 那么表面 S 。 4、正四面体的结论 :设正四面体的棱长为 a ,则这个正四面体的 (1) 全面积 :S 全= 3 2a ; (2) 体积 :V= 32 12 a ; (3) 对棱中点连线段的长 :d= 2 2 a ; (4) 对棱互相垂直。 (5) 外接球半径 :R= 6 4 a; (6)
热门知识
空间几何体的结构习题-
话题: 结构设计bluephoenix
精华知识
空间几何体的结构习题-
话题: 结构设计noerror1234
最新知识
空间几何体的结构习题-
话题: 结构设计engineerzhy
空间几何体的结构习题知识来自于造价通云知平台上百万用户的经验与心得交流。 注册登录 造价通即可以了解到相关空间几何体的结构习题最新的精华知识、热门知识、相关问答、行业资讯及精品资料下载。同时,造价通还为您提供材价查询、测算、询价、云造价等建设行业领域优质服务。手机版访问:空间几何体的结构习题
- 郑州航空港区的空间结构
- 建筑上什么叫空间结构
- 二氧化氮空间结构
- 什么叫空间布局结构
- 什么是城市空间结构
- 群落具有什么空间结构
- CO2空间结构
- 空间网格结构技术规程jgj72019
- 空间网格结构技术规程jgj7-2019
- 单层空间网壳结构
- 基于压电堆驱动器的喷嘴挡板式气体控制阀
- 分形DGS单元结构设计及其在微带电路中的应用
- 磷铵技术改造五大磷肥工程的建议
- 以大豆油多元醇制备的硬质聚氨酯泡沫塑料的性能
- 逆变TIG焊机接触引弧电路的设计(引弧电路)
- 应用模糊数学理论对公路工程建设项目方案的综合评价
- 可替代现有隔热保温材料的新型材料
- 以贯穿项目为核心载体的建筑工程技术专业素材库建设
- 多逆变器太阳能光伏并网发电系统的组群控制方法
- 影响萘高效减水剂与普通硅酸盐水泥适应性的关键因素
- 在全县非煤矿山和危化企业安全生产工作会议上的讲话
- 中国工程造价咨询业的发展趋势
- 支持并行工程和智能CAPP的制造资源建模技术
- 中共重庆市委重庆市人民政府关于建设平安重庆的决定
- 智能建筑工程报警与电视监控系统前端设备的安装施工
- 在“建筑节能与居住舒适”专题技术交流会议上的讲话
- 以MSP430FW427为核心的远程数字水表设计



