
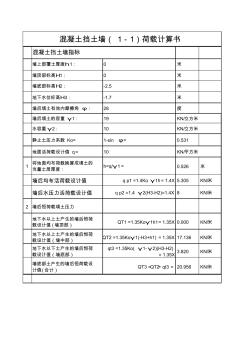
墙上部覆土厚度h1: 0 米 墙顶部标高H1: 0 米 墙底部标高H2: -2.5 米 地下水位标高H3: -1.7 米 墙后填土有效内摩擦角 φ: 28 度 墙后填土的容重 γ1: 19 KN/立方米 水容重γ2: 10 KN/立方米 静止土压力系数 Ko= 1-sin φ= 0.531 地面活荷载设计值 q= 10 KN/平方米 1 将地面均布荷载换算成填土的 当量土层厚度: h=q/γ1= 0.526 米 墙后均布活荷载设计值 q p1 =1.4Ko γ1h=1.4X 5.305 KN/米 墙后水压力活荷载设计值 q p2 =1.4 γ2(H3-H2)=1.4X 8 KN/米 2 墙后恒荷载填土压力 地下水以上土产生的墙后恒荷 载设计值 (墙顶部) QT1 =1.35Koγ1h1=1.35X 0.000 KN/米 地下水以上土产生的墙后恒荷 载设计值(墙中部) QT2 =1.35Ko


第十章 弯曲梁的设计 第一节 梁平面弯曲的概念和弯曲内力 一、弯曲的概念 工程实际中,存在大量的受弯曲杆件,如火车轮轴,桥式起重机大梁。如图 10.1.1,图 10.1.2所示,这类 杆件受力的共同特点是外力(横向力)与杆轴线相垂直,变形时杆轴线由直线变成曲线,这种变形称为弯 曲变形。以弯曲变形为主的杆件称为梁。 图 10.1.1 火 车 轮 轴 图 10.1.2 起 重 机 大 梁 工程中常见的梁,其横截面通常都有一个纵向对称轴,该对称轴与梁的轴线组成梁纵向对称面。如图 10.1.3 所示。 图 10.1.3 梁的纵向对称 如果梁上所有的外力都作用于梁的纵向对称平面内,则变形后的轴线将在纵向对称平面内变成一条平 面曲线。这种弯曲称为平面弯曲。平面弯曲是弯曲问题中最基本、最常见的,所以,这里只讨论平面弯曲 问题。 二、梁的计算简图及基本形式 梁上的荷载和支承情况比较复杂,为便与分析和计算,
热门知识
焊缝剪力计算-
话题: 工程造价152****3051
-
话题: 工程造价maojialdcr
精华知识
焊缝剪力计算最新知识
焊缝剪力计算-
话题: 工程造价a542381421a
-
话题: 建筑施工yuhuashi1988
-
话题: 工程造价152****1014
- 靠近墙角的焊缝怎么焊接
- 立焊的焊缝标准
- 中,厚板焊缝坡口选择原则
- 桩加强箍焊缝如何计算
- 怎么算钢结构焊缝长度量
- 怎样的焊缝算是好的
- 支柱焊缝与环形焊缝的区别
- 直角焊缝应力计算
- 角焊缝要不要开坡口
- 角焊缝尺寸根据什么确定
- 云计算技术在城市轨道交通运营指挥管理系统中的应用
- 有源配电网设备利用率影响因子体系及其价值计算方法
- 云计算对企业信息化系统建设和运营的影响分析和改进
- 圆形隧道反向曲线隧道中心线两种偏移计算方法的比较
- 引黄济临供水工程一级泵站圆形筒体支护结构计算分析
- 应用贵州省雨洪公式计算施工期设计洪水需注意的问题
- 引用CAD电子图在广联达工程计算软件中的应用技巧
- 圆形截面钢筋混凝土受弯构件正截面承载力的简化计算
- 工程水文与水利计算课程教学改革探索
- 云计算技术在计算机数据处理中的应用分析与发展对策
- 云南电网工程2013版建设预算费用构成及计算程序
- 圆钢管混凝土T型焊接节点应力强度因子计算方法
- 节能型家用空调器季节能效比SEER测试与计算
- 圆钢管KK型搭接节点内隐藏焊缝焊接与否有限元分析
- 有限元法在复杂水工结构变形分析及配筋计算中的应用
- 应用PC—1500机计算水工建筑物厚壁结构的内力
- 高层住宅楼施工组织设计(框架剪力墙)



